Equilibragem no local

Neste artigo são referidos alguns conceitos associados à equilibragem no local e apresentados alguns casos práticos de aplicação.

1 Equilibragem no local – Conceitos gerais

1.1 Introdução

O desequilíbrio dos rotores é um problema que se torna tanto mais importante quanto maior é a potência e a velocidade das máquinas. É uma das causas mais frequente de vibrações nos equipamentos rotativos. A equilibragem torna-se necessária para evitar o aparecimento de fendas, evitar cargas excessivas nas chumaceiras e prolongar a vida útil dos equipamentos.

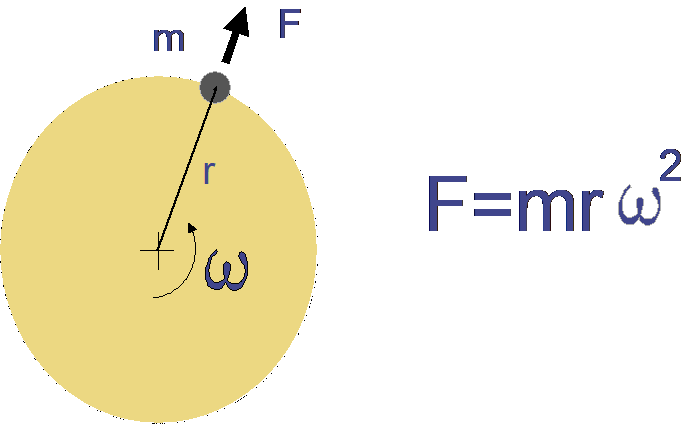
Figura 1 – Equilibragem no local – a força centrifuga

A equilibragem é a operação através da qual se melhora a distribuição da massa de um rotor, de modo a que no seu funcionamento, não apareçam forças centrifugas excessivas.

Descreve-se em seguida a forma como se deve medir o desequilíbrio de um rotor e como determinar se ele necessita de equilibragem. Descrevem-se também procedimentos de equilibragem.

1. 2 O desequilíbrio no espectro de frequência

No Espectro de Frequência, o desequilíbrio tem o efeito de provocar o aumento da componente à velocidade de rotação. Isto deve-se ao facto da massa desequilibrada acompanhar o rotor na sua rotação e portanto assim se manifestar a 1xRPM.

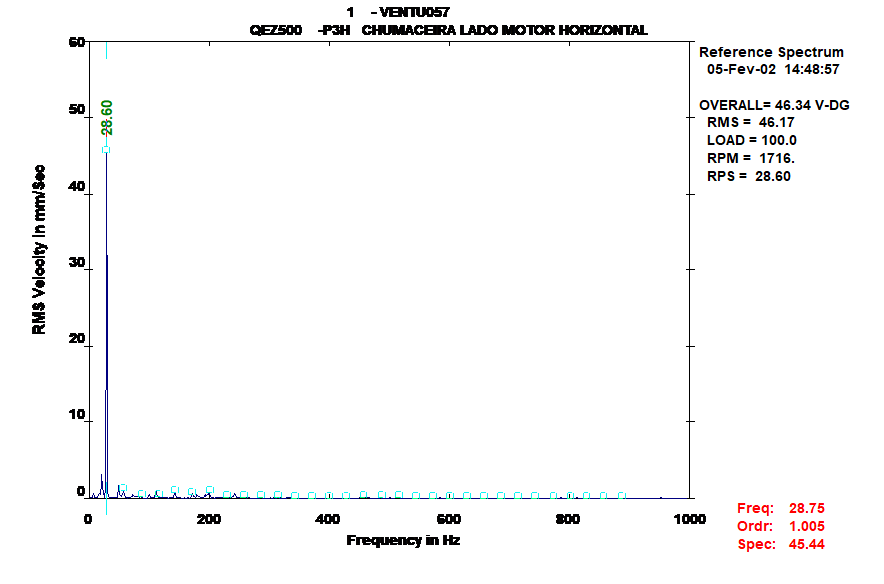
Figura 2 – equilibragem no local – o espetro de frequência obtido com um analisador de vibrações

Para identificar a causa das vibrações excessivas, é muito importante realizar uma análise de vibrações, antes de começar a operação de equilibragem.

A ilustração mostra um espectro, em velocidade, onde o problema é um desequilíbrio, como é indicado a partir do pico à velocidade de rotação. Se o rotor estiver desequilibrado, o pico a 1xRPM normalmente dominará o espectro. As componentes a 2x e 3x RPM também se notam frequentemente.

Na figura a seguir apresentada, também se vê a redução de vibrações, depois equilibragem, para aproximadamente 1/5 do nível original.

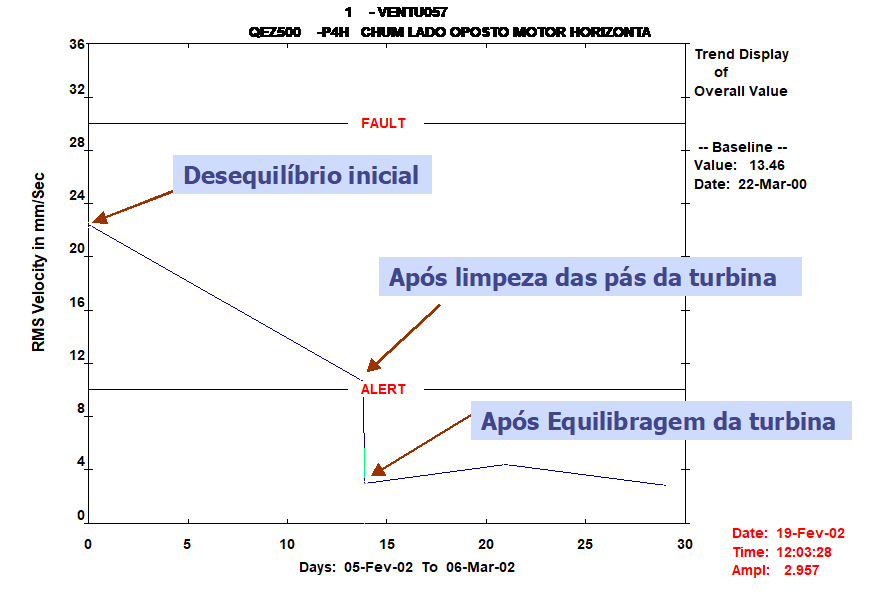
Figura 3 – Equilibragem no local – o resultado da equilibragem

Para se perceber como corrigir o desequilíbrio, vai-se passar a descrever as forças envolvidas e terminologia de acordo com a ISO 1940.

De acordo com esta norma, podem ocorrer três tipos de desequilíbrio:

Estático (ou de força)
Momento (ou binário)
Dinâmico

1. 3 O desequilíbrio estático

O caso mais simples de desequilíbrio ocorre num disco de massa M, simétrico em volta do seu eixo de rotação. É o caso de muitos ventiladores. Se uma pequena massa m (gramas) for fixa no disco a uma distância r (milímetros) do eixo, ele fica desequilibrado. A localização do desequilíbrio é frequentemente determinada, apoiando o veio em duas lâminas. Por esta razão, é frequentemente denominado de desequilíbrio estático (ou de um plano).

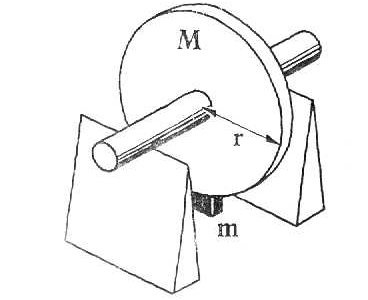
Figura 4 – equilibragem no local – o desequilíbrio estático

A força centrifuga, gerada pela massa quando o disco roda à velocidade , é dada pela fórmula:

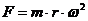
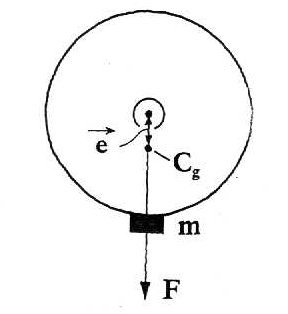
Figura 5 – equilibragem no local – a força centrifuga no desequilíbrio estático

Esta força é equivalente à força gerada por uma pequena excentricidade e, entre o centro de gravidade do disco e o eixo de rotação:

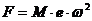
O desequilíbrio, U, é definido pela fórmula:

U=m.r

O desequilíbrio específico é achado dividindo-se o valor do desequilíbrio pela massa do rotor.

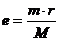
Se:

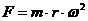
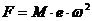
tem-se que:

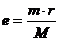
O desequilíbrio estático é definido como sendo uma excentricidade do centro de gravidade, causada por uma massa pontual a um determinado raio do eixo de rotação. Para repor o centro de gravidade no centro de rotação, é necessária uma massa de valor igual, colocada 180 graus em oposição à massa de desequilíbrio e no mesmo raio, ou em alternativa remover a massa desequilibrante. Isto, na prática, significa que um desequilíbrio estático se corrige num plano.

No dia a dia, encontram-se muitos rotores que podem ser considerados como um disco. É o caso de muitos ventiladores ou mós. É normal considerar os rotores cujo diâmetro seja 7 a 10 vezes maior que a sua largura, como discos.

1. 4 Equilibragem no local – Desequilíbrio de momento

É frequente existirem rotores em que o diâmetro não é 7 a 10 vezes maior que a sua largura, como no caso dos motores elétricos. Este facto dá lugar a desequilíbrios de momento ou dinâmicos.

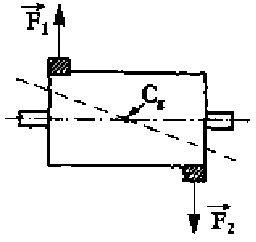
Figura 6 – equilibragem no local – a força centrifuga no desequilíbrio de momento

No caso de um cilindro, como se vê na figura, é possível ter duas massas iguais, colocadas simetricamente em relação ao centro de gravidade. O rotor está equilibrado estaticamente, ou seja, o seu centro de gravidade não está excêntrico. Contudo, quando começa a rodar, as duas massas provocarão forças que gerarão um binário. Isto provoca fortes vibrações. O desequilíbrio só pode ser corrigido, medindo as vibrações com a máquina em andamento e depois colocando massas em dois planos.

1.5 Equilibragem no local – Desequilíbrio dinâmico

Normalmente, o desequilíbrio num rotor é a combinação de um desequilíbrio estático com um de momento, ou seja, é um desequilíbrio dinâmico. Para corrigir o desequilíbrio, é necessário medir as vibrações com o veio em rotação e depois colocar massas em dois planos.

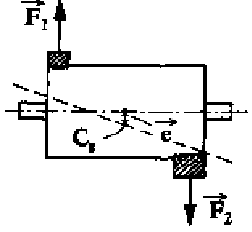
Figura 7 – equilibragem no local – a força centrifuga no desequilíbrio dinâmico

1.6 Norma ISO 21940-11 Classificação dos rotores

Até agora falou-se em desequilíbrios sem definir que é excessivo e o que é aceitável. Idealmente, uma máquina equilibrada não deveria ter desequilíbrio nenhum. Na prática isto não é realizável. Para diferentes tipos e dimensões de máquinas, o nível de vibrações considerado como excessivo varia consideravelmente: por exemplo o nível de vibrações aceitável numa cambota de um carro destruiria um giradiscos.

A figura mostra parte da classificação adotada pela “ISO 21940-11:2016 Mechanical vibration – Rotor balancing Part 11: Procedures and tolerances for rotors with rigid behaviour”. Esta classificação associa um grau a cada tipo de rotor. Mais à frente vai-se ver como usando este grau conjuntamente com um gráfico se determina o desequilíbrio aceitável.

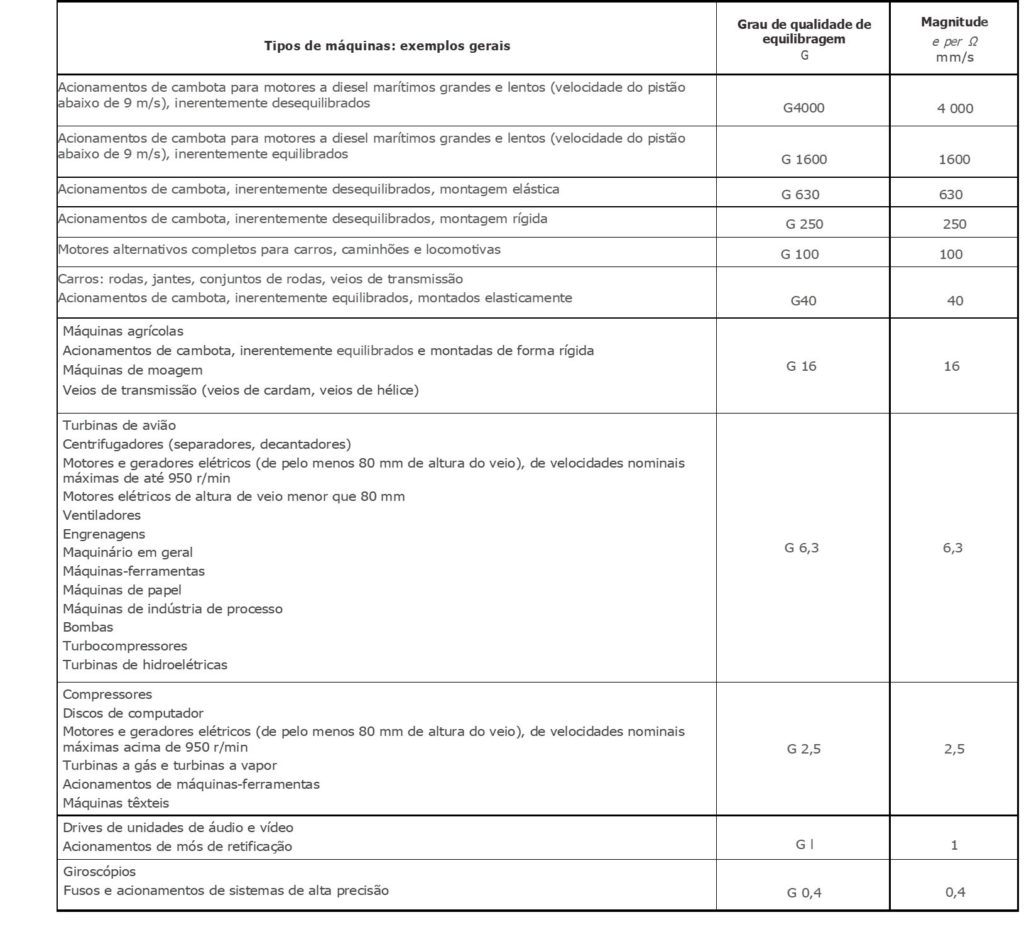
Considera-se um rotor rígido aquele cuja máxima velocidade é inferior a metade da primeira frequência natural.

1.7 Norma ISO ISO 21940-11 : desequilíbrio aceitável

O gráfico apresentado na norma mostra o máximo desequilíbrio residual admissível para diferentes tipos de rotores. A figura mostra uma versão simplificada do gráfico da ISO 21940-11 .

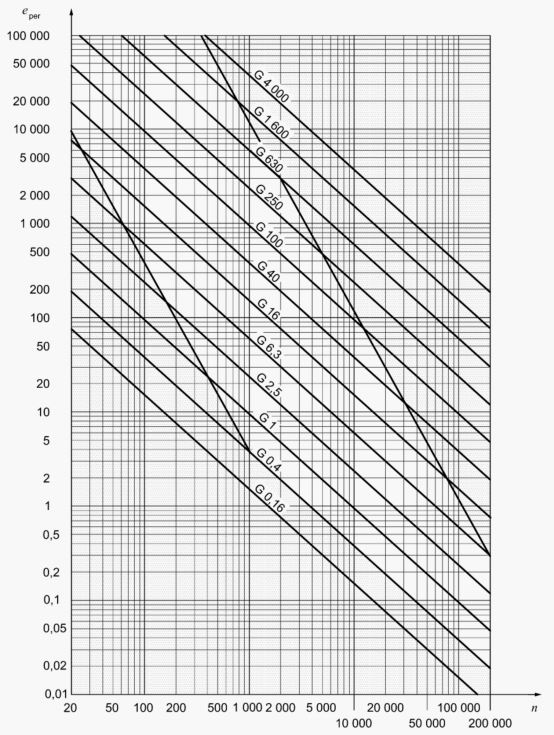
O eixo vertical mostra o máximo desequilíbrio residual admissível em g.mm/kg ou micron.

Quando se utiliza esta norma, o primeiro passo é classificar o rotor. Como exemplo escolhemos um ventilador (Grau 6.3), cuja velocidade máxima é 3000 RPM. Para usar o gráfico procede-se da seguinte maneira:

Traçar uma linha vertical a partir da velocidade máxima de rotação da maquina, ate se intersectar alinha obliqua correspondente à classe do rotor.

Traçar uma linha horizontal a partir do ponto de intersecção atras referido.

Ler no eixo vertical o máximo desequilíbrio residual admissível, neste caso, 20 (g.mm/kg ou micron).

Este resultado significa que para cumprir o Grau de Qualidade 6.3, o desequilíbrio residual admissível não deve ser maior que 20 depois da equilibragem. Mais adiante se verá como é que este valor é na prática usado.

1.8 Rotores com massas distribuídas assimetricamente

O calculo do máximo desequilíbrio residual admissível parte do principio que a massa do rotor está distribuída simetricamente. Se isto não for o caso, o cálculo é uma pouco mais complicado.

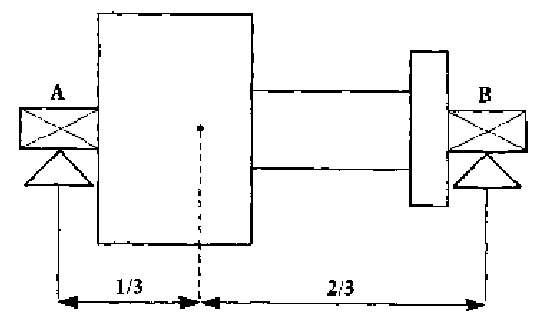
A ISO ISO 21940-11 atribuiu a Classe 6,3 para o rotor do exemplo atrás referido. À velocidade de rotação de 3000RPM, o desequilíbrio admissível é de 20 micron.

Num rotor perfeitamente equilibrado, quando em rotação, actuarão forças iguais em ambos os seus extremos.

Se a forma do rotor for a que se vê na figura, as forças em cada topo serão iguais, mas o desequilibro admissível em cada chumaceira será diferente. A posição do centro de gravidade divide o rotor na razão 1/3:2/3. Assim o desequilíbrio residual admissível na chumaceira A é 2/3 do total admissível, ou seja, aproximadamente 14 mm, e na chumaceira B, 7 mm.

Isto na prática significa que no caso de rotores muito assimétricos, como e frequentemente o caso de ventiladores, na maioria das vezes, pode-se atribuir o total do desequilíbrio residual admissível à chumaceira junto à turbina.

2 Procedimentos de equilibragem no local

2.1 Equilibragem no local na prática

Regra geral, para qualquer máquina, pode-se definir um nível de vibrações, considerado como aceitável. Este nível é obtido a partir de medições feitas, quando a máquina se encontra em boas condições de funcionamento, noutras máquinas similares ou em normas.

As vibrações geradas pelos desequilíbrios dependem não só do valor do desequilíbrio, mas também da mobilidade da máquina.

Com um equipamento portátil de equilibragem no local, mede-se a amplitude das vibrações e um ângulo, que pode ser usado para calcular a posição onde se deve colocar a massa de correção.

2.2 Equilibragem no local – Descrição genérica

Equilibra-se um rotor colocando uma massa de correção de um certo valor, numa posição em que compense o seu desequilíbrio, ou seja, a 180 graus em relação a ele. Para se fazer isto, precisa-se de duas informações:

O peso da massa de correção
A posição onde se deve colocar esta massa

Para se fazer a equilibragem é, portanto, necessário determinar estes dois valores.

Existem diversos métodos e equipamentos que permitem fazer isto. A sua aplicação em cada caso depende dos condicionalismos existentes.

O método de equilibragem mais frequente usa um equipamento que permite medir a amplitude e a fase da componente à velocidade de rotação.

A amplitude da componente à velocidade de rotação, é medida com um analisador de vibrações. A fase pode ser medida com um estroboscópio ligado a um Analisador de Espectro de Frequência ou com um sistema que dê uma leitura digital do seu valor.

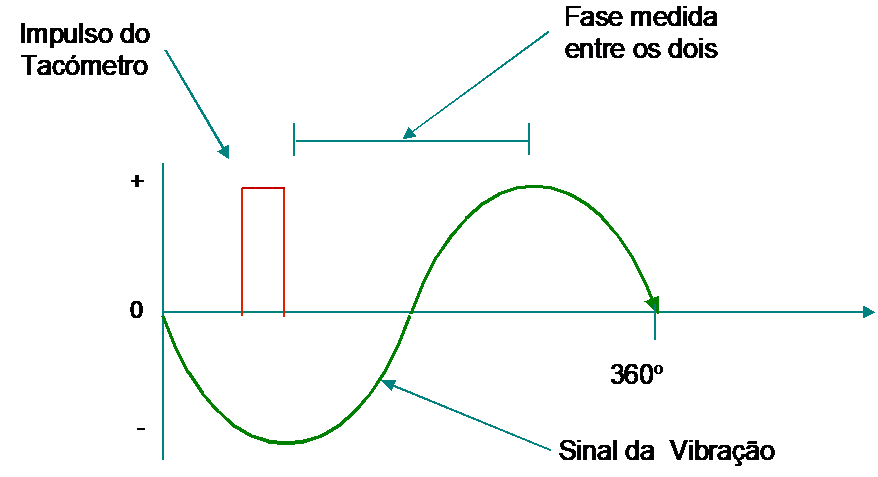
Figura 8 – equilibragem no local – medição de amplitude e fase

Uma marca no rotor origina um sinal uma vez por rotação, enviando um impulso para o medidor de fase.

Um acelerómetro montado na chumaceira mede a vibração. O sinal elétrico gerado no acelerómetro é analisado em frequência. O medidor de fase compara a fase entre os dois sinais. O medidor de vibrações mostra a amplitude da componente à velocidade de rotação. Têm-se assim, qualquer que seja o sistema de medida, dois valores:

Fo, o ângulo de fase das vibrações
Vo, a vibração filtrada causada pelo desequilíbrio

2.3 Equilibragem no local num plano com medição de fase

Depois de se ter medido a amplitude (Vo) e a fase (Fo) das vibrações com a máquina nas condições iniciais, ou seja, desequilibrada, coloca-se uma Massa de Ensaio ( Mt) no rotor. Mede- se então:

F1, a fase com a massa de ensaio montada

V1, a amplitude das vibrações com a massa de ensaio montada

Conhecendo-se os efeitos da massa de ensaio pode-se calcular o valor e a posição de colocação da massa de correcção. Este calculo pode ser feito manualmente, com um diagrama vectorial, ou com uma calculadora, em que portanto se obtém:

Mc massa de correcção

Fc angulo de correcção

Coloca-se portanto a massa de correcção no rotor e mede-se novamente a amplitude e fase das vibrações. Se não se conseguir reduzir as vibrações para um valor aceitável, tem que se continuar a operação de equilibragem.

Foi portanto definido o procedimento para se realizar a equilibragem. Todavia, para poder ser seguido, é necessário saber:

Como escolher uma massa de ensaio adequada
Como traçar o diagrama vectorial

Como usar uma calculadora e um programa de equilibragem
Como assegurar que se obtêm medições adequadas
Onde colocar a massa de correcção

2.4 Equilibragem no local – A escolha da massa de ensaio

Os cálculos são feitos com base nos efeitos da massa de ensaio nas condições iniciais do rotor. É portanto importante escolher uma massa de ensaio adequada para se ter bom resultado.

Viu-se que o desequilíbrio especifico, e, é definido do seguinte modo

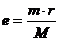
onde

m = massa de desequilíbrio residual aceitável

r = raio a que esta colocado o desequilíbrio

M = massa do rotor

Tem-se portanto:

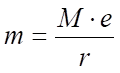
Esta equação pode assim ser usada para calcular o máximo desequilíbrio residual aceitável depois da equilibragem.

Tome-se, como exemplo, um rotor da classe 6,3 e com a velocidade máxima de 3000 RPM. Já atrás se viu que o máximo desequilíbrio residual aceitável, neste caso, e de 20 mm. Se a massa do rotor (M) for de 50 kg e o raio (r) onde e montada a massa de correcção for de 100 mm, tem-se:

m=50 x 20/100= 10 g

Recomenda-se que se escolha uma massa de ensaio que seja 5 a 10 vezes maior, que o máximo desequilíbrio residual aceitável. Então, neste exemplo, a massa de ensaio devera ter um valor entre 50 e 100 gramas.

A experiência mostra que quando a massa de ensaio e calculada desta maneira tende sempre a ser demasiado pequena. Contudo é melhor ter uma massa de ensaio pequena do que arriscar danificar o rotor.

Estas regras são guias para um principiante poder começar com resultados aceitáveis. Com o aumentar da experiência começa-se a conhecer o valor das massas de ensaio adequadas a cada caso.

2.5 Os ensaios

Como resultado dos ensaios obtiveram-se as seguintes medidas:

Vo e Fo , a vibração e fase inicial
A1 e F1 , a vibração e fase com a massa de ensaio

Para calcular a massa de correcção e o seu angulo, esta informação é representada vectorialmente do modo como se mostra na figura e a seguir é explicado:

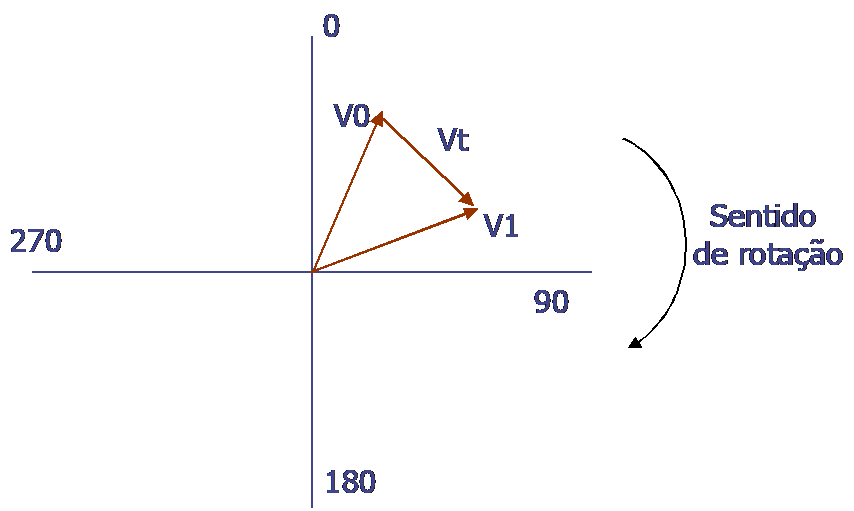
Desenhar um vector que represente a amplitude e fase das vibrações com a massa de ensaio montada. Chama-se a este vector V1.

Desenhar um vector da ponta de Vo para a ponta de V1 e assinalar o sinal da seta de modo a evidenciar a direcção de Vo para V1 .Chame-se a este vector, que representa o efeito da massa de ensaio, Vt.

Desenhar um vector paralelo a Vt, na mesma direcção, mas começando na origem das coordenadas. Chama-se também a este vector Vt .

Prolongar o vector Vo, através da origem das coordenadas, mas na direcção oposta. Chama-se a este vector –Vo.

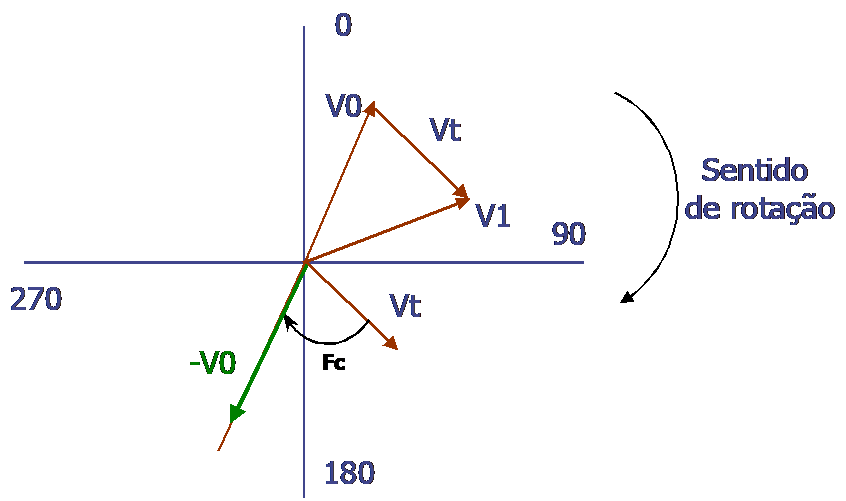
(Vo representa o desequilíbrio inicial. -Vo representa a posição e valor da massa requerida para o corrigir. O efeito da massa de ensaio é representado pelo vector Vt).

Imagine-se que se roda o vector a tracejado Vt até coincidir com Vc. O ângulo Fc representa o ângulo da rotação requerida. A direcção de Fc é vista considerando os eixos de referência. No exemplo acima, Fc é positivo.

(Para corrigir o desequilíbrio, tem que se colocar uma massa com o mesmo valor do desequilíbrio, mas em oposição, ou seja, a 180 graus da posição da massa desequilibrante. Para equilibrar o rotor, a massa de correcção tem de provocar uma força igual à do desequilíbrio, mas na direcção oposta).

Imagine-se agora o vector Vt foi rodado de modo a coincidir com o vector Vc. Para equilibrar o rotor tem de ter a mesma amplitude de Vo. Assim, o próximo passo, é aumentar ou diminuir o comprimento de Vt de modo a ter a mesma dimensão que o vector Vc .Isto é feito partindo-se do principio que a amplitude da vibração é proporcional à massa do desequilíbrio. Tem-se assim que:

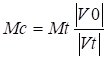
Esta equação permite calcular o valor de Mc. Para exemplificar veja-se o problema seguinte:

2.6 Ensaio de confirmação

Apesar do cuidado na selecção da massa de ensaio, pode acontecer que não se obtenham resultados adequados para os cálculos. Antes de usar os efeitos da massa de ensaio para calcular a massa de correcção, é muito importante verificar que os resultados são adequados.

Se a diferença em fase DF for menor que 25 graus, a massa de ensaio tem de ser aumentada ou mudada de posição e o ensaio tem de ser repetido.

Se a diferença em fase DF for maior que 25 graus, os valores medidos podem ser usados para calcular a massa e ângulo de correcção.

	Delta V< 25%	Delta V> 25%
Delta F<25º	Aumentar Massa de Teste	Mudar posição de Massa de Teste
Delta F>25º	Continuar	Continuar

Para explicar a razão pela qual uma mudança de menos de 25 graus no ângulo de fase requer um ajustamento na massa de ensaio e novas medições, considere-se as duas situações que podem ocorrer:

Neste caso a amplitude do vector Vt é muito pequena porque a massa de ensaio não mudou as condições iniciais. Com uma precisão de medição de fase de ± 1º e apenas uma pequena mudança em fase o erro relativo pode ser muito grande. Isto provocaria um grande erro relativo no comprimento de Vt. Se então ajustarmos o vector Vt para ter a mesma amplitude que Vo arriscamo-nos a que os erros cometidos provoquem uma deficiente equilibragem.

Assim neste caso é conveniente aumentar a massa de ensaio e repetir as medições.

Mudar de posição a massa de ensaio e repetir as medições deverá originar bons resultados.

2.6 Correção do desequilíbrio

A posição da massa de correção é determinada a partir da posição da massa de ensaio no rotor. O ângulo de correção pode ser positivo ou negativo.

Se o ângulo Fc for positivo, é medido a partir da posição da massa de ensaio, na direcção da rotação da máquina.

Um ângulo negativo é medido na direção oposta. Quando a massa de correção estiver montada, remove-se a massa de ensaio. A massa é montada no mesmo raio em que estava a massa de ensaio.

2.7 Equilibragem em dois planos

Foram referidos os princípios de funcionamento e utilização de um equipamento de equilibragem no local, e como fazer a equilibragem num plano.

Os princípios para equilibragem em 2 planos são muito semelhantes aos da equilibragem em 1 plano.

O procedimento de equilibragem em dois planos consiste nos seguintes passos:

Fazer uma Análise em Frequência nas duas chumaceiras.
Registar a Amplitude e a Fase das vibrações nas duas chumaceiras.
Montar a Massa de Ensaio no Plano 1.
Com a Massa de Ensaio no Plano 1, medir e registar a Amplitude e Fase das vibrações nas duas chumaceiras.
Marcar a posição da Massa 1 e removê-la.
Montar a Massa de Ensaio no Plano 2.
Com a Massa de Ensaio no Plano 2, medir e registar a Amplitude e Fase das vibrações nas duas chumaceiras.
Calcular as Massas de Correcção e ângulos usando um programa adequado.
Marcar a posição da Massa no Plano 2 e removê-la.
Montar as Massas de Correcção nos dois planos.
Medir a vibração residual nas duas chumaceiras.

Se o nível de vibrações não for aceitável repetir os passos anteriormente descritos.

3 Alguns casos especiais

3.1 – A equilibragem de um ventilador com pás

A figura mostra a posição das pás de um ventilador. Se, como resultado da operação de equilibragem, a massa de correção calculada for de 2 gramas para colocar a um ângulo de 100 graus, parece impossível montá-la. A solução é dividir a massa de correção entre as pás a 72 graus e a 144 graus.

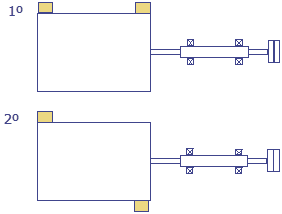
3.2 – Equilibragem de um rotor com planos de equilibragem que não estão entre chumaceiras

A figuras mostra um exemplo típico deste tipo de rotores. Se o seu comprimento for aproximadamente 1/7 a 1/10 do seu diâmetro, então pode-se fazer uma equilibragem num plano, escolhendo a chumaceira mais influenciada pela massa de ensaio.

Para os outros casos é necessário usar dois planos de correcção com um dos seguintes métodos:

1 – Usar duas vezes o procedimento de equilibragem num plano.

Primeiro executar uma equilibragem estática com a massa de ensaio dividida em duas massas iguais e montadas em fase. Medir na chumaceira mais influenciada pelas massas de ensaio. A massa de correcção calculada também deve ser dividida em duas iguais.

Em seguida realiza-se novamente uma equilibragem estática, mas desta vez montando-as a 180 graus uma da outra, nos dois planos. As forças em volta do centro de gravidade do rotor deverão ser iguais e de direcção oposta. A massa de correcção calculada também deve ser dividida num par, montadas a 180 graus uma da outra.

Notar que a massa de ensaio usada nos cálculos deve ser a soma do par de massas de ensaio usado.

2 – Executar o procedimento de equilibragem em dois planos usando os planos de medição e correcção como indicado na figura.

Notar que as massas de ensaio podem ser montadas tal como no procedimento normal de equilibragem em dois planos, ou seja, arbitrariamente no circulo de correcção.

3.3 – A massa e o raio de correção

A geometria do rotor às vezes implica que não se possa montar a massa de correcção no mesmo raio que a massa de ensaio. Para corrigir o desequilíbrio, usa-se uma relação já referida:

A equação mostra que e M é proporcional a m r. Se o produto m r for mantido constante, e M também se mantém constante, ou seja:

e.M=m.r

3.4 – Equilibragem num plano sem medição de fase

Este método permite determinar o valor e posição do desequilíbrio sem medição de fase.

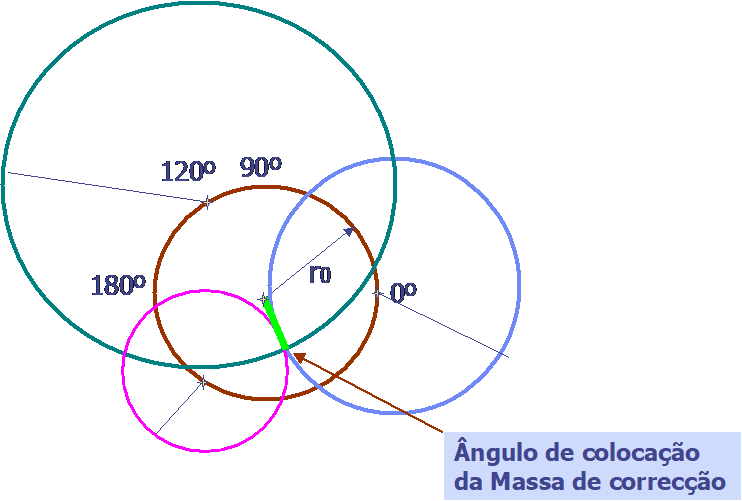
Neste método, como nos outros, todas as medições são feitas à frequência de rotação.

Primeiro mede-se o desequilíbrio inicial. A seguir utiliza-se uma massa de ensaio, para introduzir um desequilíbrio conhecido, fixando-se ao rotor, no mesmo raio onde se vai colocar a massa de correcção final.

Realizam-se três ensaios com a massa de ensaio colocada no rotor a 0, 120 e 240 graus. Faz-se então a construção geométrica que se vê na figura, para determinar a Massa de Correcção. Primeiro traça-se um circulo de raio igual ao desequilíbrio inicial Vo, marcando-se nele os pontos a 0, 120 e 240 graus.

Com centro nestes pontos, e com raio igual à vibração medida quando a Massa de Ensaio estava colocada no ponto correspondente do rotor, traçam-se três círculos, que se vão intersectar num ponto. Este ponto define o valor da Massa de Ensaio Vt. Pode-se então calcular o seu valor.

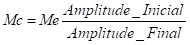
Caso a Massa de Ensaio não seja colocada nas posições atrás referidas (0, 120, 240 graus) então na construção gráfica a posição dos centros dos círculos V1, V2 e V3 mudará de modo a corresponder à montagem no rotor.

Para implementar este método pode-se utilizar um medidor de Nível Global de Vibrações desde que a vibração predominante seja à frequência da velocidade de rotação.

4 – Verificação do desequilíbrio residual

Depois da equilibragem ser dada por concluída, pode-se determinar o desequilíbrio residual.

Isso normalmente é feito utilizando o equipamento de equilibragem adequada, como o já atrás descrito.Com as vibrações residuais realizam-se novos cálculos para determinar as massas de correcção necessárias para as eliminar. O valor destas massas vezes o raio de correcção é o desequilíbrio residual.

Caso 1 Equilibragem no local de ventilador

Um ventilador com a configuração igual à ilustrada na Figura 9, apresentava níveis vibrométricos bastantes elevados. A amplitude vibrométrica mais elevada foi registada no apoio do ventilador do lado oposto ao acionamento, segundo a direção Horizontal (12,01 mm/s RMS).

Figura 9 – Equilibragem no local – Fotografia da unidade de acionamento

A análise espectral efetuada aos espectros de frequências recolhidos revelou que a severidade vibrométrica, existente no apoio do ventilador do lado oposto ao acionamento, era influenciada pela amplitude de frequência de funcionamento e pela amplitude das harmónicas da mesma (Figura 10).

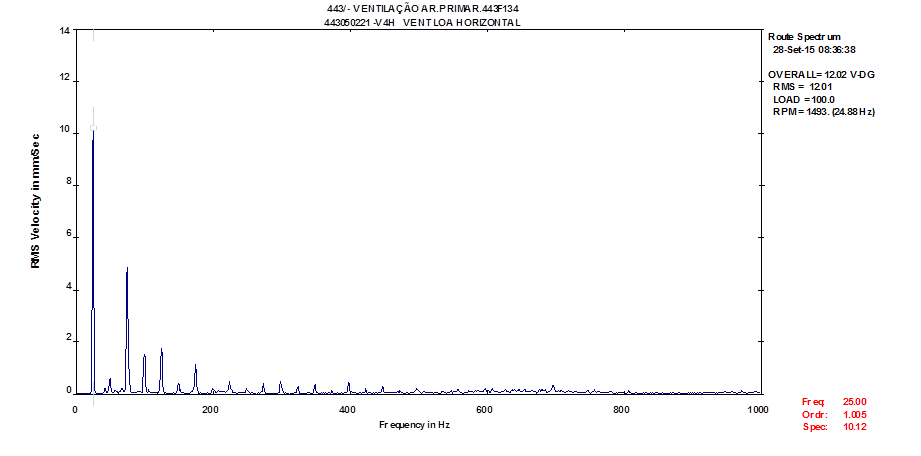
Figura 10 – Equilibragem no local – Espectro de frequências recolhido no apoio do ventilador do lado oposto ao acionamento

Caso 1 – Análise da informação

Esta característica revela, por um lado, a presença de uma condição associada ao desequilíbrio, mas também a folgas excessivas. Esta condição já era conhecida e foi confirmada numa inspeção efetuada ao alojamento do referido rolamento.

No entanto, apesar da condição de folgas identificada, os níveis vibratórios em presença na máquina não apresentavam valores tão elevados como os verificados na última inspeção. Face ao referido, considerou-se que, para além da condição de folgas excessivas, a condição de equilíbrio do rotor se tinha deteriorado, motivo pelo qual as amplitudes da componente a 1xRPM e respetivas harmónicas sofreram um agravamento significativo. Deste modo, por forma a prolongar o funcionamento da máquina até à paragem geral para manutenção da instalação, optou-se por efetuar uma equilibragem no local numa tentativa de diminuir a amplitude da componente a 1xRPM e, ao minimizar a força excitadora, diminuir também a amplitude das harmónicas da referida componente.

Caso 1 – Ações desenvolvidas

As ações de equilibragem desenvolveram-se num plano, tendo sido aplicadas as seguintes massas de correção: 120 gr @ 257º e 90 gr @ 272º. No gráfico da Figura 11, encontra-se representada a evolução da componente a 1xRPM durante a equilibragem efetuada.

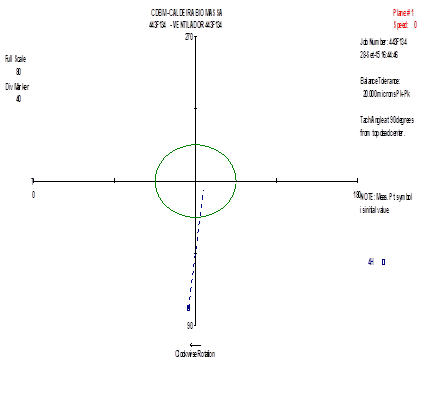
Figura 11 – Equilibragem no local – Evolução da componente a 1xRPM durante a equilibragem

Após a equilibragem, registou-se uma diminuição muito significativa, não só da componente a 1xRPM mas também da amplitude das suas harmónicas como se pode observar na Figura 12.

Figura 12 – Equilibragem no local – Espectros em cascata de frequências recolhidos antes e após a equilibragem

A equilibragem efetuada no local permitiu reduzir significativamente a severidade vibrométrica a que a máquina se encontrava submetida. A redução que se verificou foi originada não só pela diminuição da amplitude da componente a 1xRPM, mas também devido à diminuição da amplitude das suas harmónicas. Com a melhoria da condição dinâmica da máquina, foi possível prolongar o seu funcionamento até à paragem geral programada para manutenção da instalação, na qual se efetuará a substituição das chumaceiras do ventilador para eliminação da causa da condição de folgas excessivas identificada.

Caso 2 Equilibragem no local de ventilador

A principal causa de vibrações excessivas em ventiladores está associada a desequilíbrio. Acumulações de resíduos e desgaste do rotor são apenas algumas das fontes de desequilíbrio.

Na sequência de uma inspeção efetuada a um conjunto de ventiladores foi diagnosticado, através da medição de vibrações, que um dos ventiladores apresentava valores de vibrações elevados. Após diagnosticar que a principal fonte dos elevados níveis vibrométricos estavam associados a desequilíbrio, foi proposta uma equilibragem no local, tendo em vista a redução da severidade vibrométrica a que o equipamento se encontrava submetido.

O motor de 45 kW funciona a 1480 rpm que, através da transmissão por correias, aciona o ventilador a 1478 rpm.

Caso 2 ações desenvolvidas

Na Figura 13 que a seguir se apresenta, encontra-se um espectro de frequências onde é possível observar a elevada amplitude da componente a 1xrpm, originada pela condição de desequilíbrio existente no ventilador antes das ações de equilibragem.

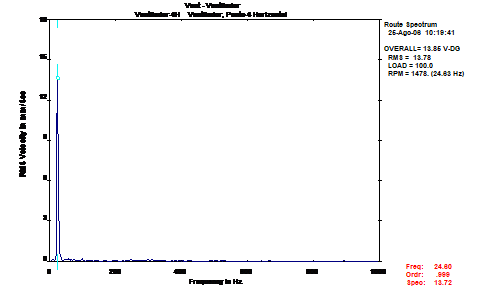
Figura 13 – Equilibragem no local – Espectro de frequências recolhido no ventilador antes da equilibragem

Após a correção do desequilíbrio, através da adição de massa ao rotor, as amplitudes vibrométricas diminuíram significativamente.

A massa para a correção de desequilíbrio foi de 4 grama colocada a 255º.

Com esta única correção, foi possível reduzir a severidade vibrométrica, por forma a que o equipamento funcionasse com valores de vibrações considerados Bons/Aceitáveis de acordo com a norma ISO10816-1

Na Figura 14, encontra-se o espectro de frequência recolhido no apoio do ventilador, após a ação de equilibragem. Comparando os espectros de frequências da Figura 13 e 14, pode-se observar a melhoria registada.

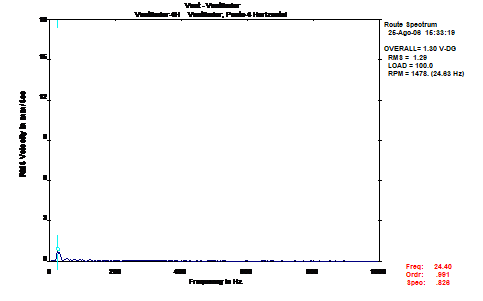
Figura 14 – Equilibragem no local – Espectro de frequências recolhido no ventilador após a equilibragem

Na Figura 15, apresenta-se o gráfico com a evolução dos valores de nível global de vibração, onde se pode constatar a melhoria significativa, após as ações de equilibragem.

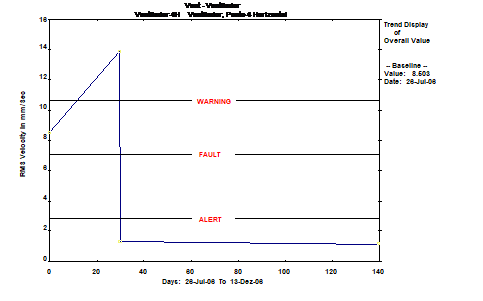
Figura 15 – Equilibragem no local – Evolução dos níveis vibrométricos ao longo das diferentes medições efetuadas

Caso 2 – Equilibragem no local – Conclusão

A equilibragem no local permite reduzir custos associados à desmontagem do rotor e envio para equilibragem em banco, com a consequente imobilização da máquina.

Com a equilibragem no local foi possível reduzir significativamente os níveis de vibração e, desta forma, aumentar a vida útil dos componentes rotativos e estruturais.

Caso 3 – Equilibragem no Local do Rotor de Um Ventilador

Um ventilador, semelhante ao ilustrado na Figura 16, apresentava níveis vibrométricos bastante elevados. O valor mais elevado (21,4 mm/s RMS) foi registado no apoio do motor do lado do acionamento, segundo a direção Vertical.

Figura 16 – Equilibragem no local – Esquema do ventilador.

A análise efetuada aos espectros de frequências recolhidos revelava que a severidade vibrométrica em presença na máquina era, sobretudo, influenciada pela amplitude da frequência de funcionamento (Figura 17). Estando esta característica associada a uma condição de desequilíbrio, optou-se por efetuar a equilibragem do rotor do ventilador no local.

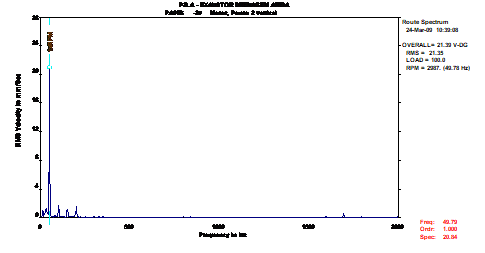
Figura 17 – Equilibragem no local – Espectro de frequência registado no apoio do motor do lado do acionamento, segundo a direção Vertical.

As ações de equilibragem desenvolveram-se a um plano e a massa de correção aplicada foi de 22 gr @ 39º.

Após a equilibragem efetuada foi possível reduzir em cerca de 91%, a amplitude da frequência de funcionamento do ventilador.

Na Figura 18, apresentada a seguir, pode observar-se a evolução dos níveis vibrométricos em presença na máquina, antes e após a equilibragem.

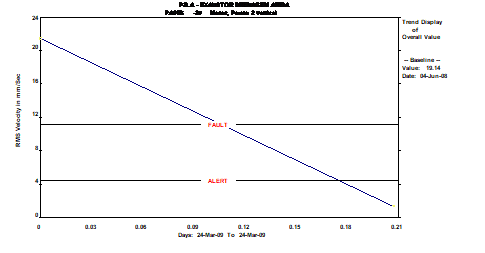
Figura 18 – Evolução dos níveis vibrométricos registada no apoio do motor do lado do acionamento, segundo a direção Vertical.

Na Figura 19 são apresentados os espectros de frequência, registados antes e após a equilibragem, através dos quais se pode verificar a significativa redução da amplitude da frequência de funcionamento.

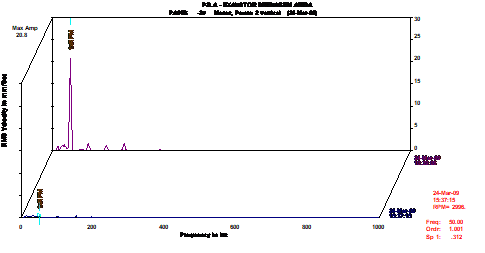
Figura 19 – Equilibragem no local – Espectros de frequências recolhidos antes e após a equilibragem.

Caso 3 Equilibragem no local – Conclusão

A equilibragem efetuada no local permitiu reduzir significativamente a severidade vibrométrica em presença. A melhoria da condição dinâmica influenciará, de forma direta, a vida útil dos componentes, com reflexo natural na fiabilidade da máquina.

Caso 4 – Equilibragem no local do rotor de um ventilador

Um ventilador após ter sido intervencionado para a substituição da turbina e dos rolamentos, apresentava valores de vibração elevados como se pode observar pelos valores apresentados na Tabela I.

Tabela I

Ponto de Medição	Nível de Vibração em mm/s RMS
1 Vertical	1,1
1 Horizontal	1,7
2 Vertical	2,7
2 Horizontal	2,4
2 Axial	1,4
3 Vertical	5,2
3 Horizontal	27,3
4 Vertical	6,5
4 Horizontal	31,6

Analisando os valores apresentados, conclui-se que, nos apoios dos ventilador (ponto 3 e 4 ), os níveis de vibração são considerados críticos. A análise espectral revelou que os níveis de vibração eram, sobretudo, influenciados pelas amplitudes da frequência de funcionamento do ventilador (21,81 Hz). Esta característica, ilustrada na Figura 20, estava associada a desequilíbrio.

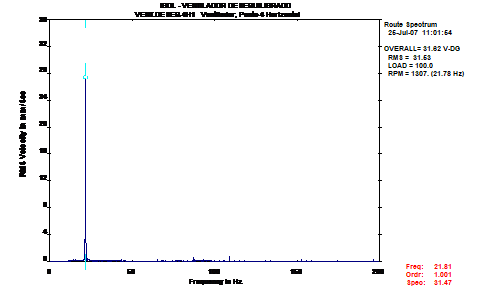
Figura 20 – Equilibragem no local – Espectro de frequência recolhido no ventilador, do lado da turbina (antes da equilibragem).

Com a equilibragem efetuada a um plano, foi possível reduzir a severidade vibrométrica associada.

As massas de correção aplicadas são as que constam na Tabela II

Tabela II

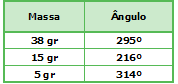
Os níveis vibrométricos registados após a equilibragem constam na Tabela III:

Tabela III

Ponto de Medição	Nível de Vibração em mm/s RMS
1 Vertical	1,3
1 Horizontal	1,1
2 Vertical	1,3
2 Horizontal	1,3
2 Axial	1,1
3 Vertical	2,3
3 Horizontal	3,9
4 Vertical	3,2
4 Horizontal	2,5

Pelos valores apresentados na Tabela III, conclui-se que os níveis de vibração após a equilibragem são, na generalidade, considerados Bons/Aceitáveis, registando-se uma redução muito significativa da severidade vibrométrica.

A Figura 21 apresenta o espectro de frequência recolhido após as ações de equilibragem.

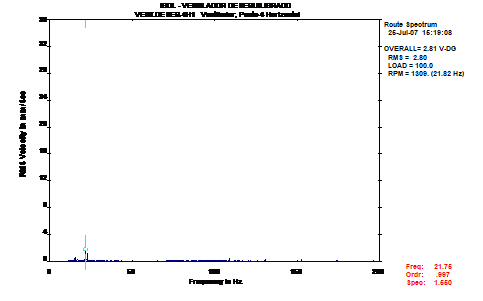
Figura 21 – Equilibragem no local – Espectro de frequência recolhido no ventilador, do lado da turbina (após a equilibragem)

Caso 4 – Equilibragem no local – Conclusão

Com a equilibragem no local, foi possível melhorar a condição dinâmica do equipamento, reduzindo os custos associados à equilibragem em banco, bem como, aumentar a vida útil dos componentes, nomeadamente rolamentos, estruturas, etc.