Identificação de frequências naturais
1 – Introdução – Identificação de frequências naturais com um analisador de vibrações
Neste artigo sobre a identificação de frequências naturais com um analisador de vibrações, são descritos diversos métodos para se determinarem frequências naturais numa máquina ou estrutura.
Sempre que se desconfia da possibilidade de ocorrem fenómenos de ressonância, ou se quer confirmar as frequências calculadas por métodos analíticos, é importante determinar experimentalmente as frequências naturais.
2 – Tipos de ensaios e condição da máquina / estrutura durante a sua realização
Os ensaios podem ser efetuados com a máquina nas seguintes condições:
- Máquina parada
- O ensaio de impacto
- A medição da resposta em frequência (FRF)
- Máquina em variação de velocidade;
- A média de retenção de pico (Peakhold)
- As ordens
- A cascada
- O bode e o Nyquist
- Máquina em funcionamento em regime estável;
- Média negativa
2.1 Identificação de frequências naturais com um analisador de vibrações – Ensaios com a máquina parada
Este tipo de ensaios tem como base o princípio de que qualquer estrutura quando está livre, vibra às suas frequências naturais. Portanto para observar as suas frequência naturais basta, por exemplo, efetuar um impacto na estrutura e observar a resposta.
Existem duas formas de observar o impacto.
A forma mais simples consiste em medir só a resposta; o designado ensaio de impacto.
A forma mais elaborada consiste em medir a Função de Resposta em Frequência (FRF). Esta é obtida utilizando um martelo instrumentado com um transdutor de força de forma a se conhecer a energia que está a ser introduzida na estrutura. Esta forma de medir as frequências naturais é mais precisa e permite a comparação dos resultados medidos com os modelos de elementos finitos e a análise modal.
A seguir podem-se ver as unidades em que a FRF pode ser formulada.
| Rigidez dinâmica | Força / Deslocamento |
| Receptância | Deslocamento / Força |
| Impedância | Força / Velocidade |
| Mobilidade | Velocidade / Força |
| Inércia dinâmica | Força / Aceleração |
| Acelerância | Aceleração / Força |
A medição da resposta em frequência (FRF) para além de uma das funções atrás descritas, proporciona informação sobre a fase das vibrações e a função coerência.
Numa medição da Função de Resposta de Frequência pode ser observado o seguinte:
- Ressonâncias – Os picos indicam a presença das frequências naturais da estrutura em teste;
- Amortecimento – O amortecimento é proporcional à largura dos picos. Quanto mais largo o pico, maior é o amortecimento;
- Modo de vibração – A amplitude e fase de múltiplas FRFs adquiridas relativamente a uma referência comum numa estrutura são utilizados para determinar a forma do modo.
A Coerência é função versus frequência, que indica quanto da saída é devido à entrada na FRF. Pode ser um indicador da qualidade da FRF. Avalia a consistência do FRF desde a medição até à repetição da mesma medição. O valor de uma função de coerência varia entre 0 e 1.
A medição de fase, define inequivocamente que estamos na presença de uma frequência natural pois, na ressonância a fase varia 180º. Caso esta variação seja inferior a 180º quer dizer que, ou a estrutura está fortemente amortecida ou então, que o movimento da estrutura na ressonância não ocorre na direção do acelerómetro e/ou do martelo.
2.2 Identificação de frequências naturais com um analisador de vibrações – Ensaios efetuados com a máquina em variação de velocidade
Nos ensaios efetuados com a máquina em variação de velocidade usam-se as forças geradas no funcionamento da máquina para excitar as suas frequências naturais.
Este ensaio pode ser efetuado em arranque ou em paragem. Se o arranque da máquina for muito rápido, é mais conveniente efetuá-lo em paragem.
2.2.1 A média de retenção de pico (Peakhold)
A média de retenção de pico (Peakhold) é a maneira mais simples de identificar frequências naturais durante a paragem de uma máquina. Funciona muito bem quando o espetro de frequência só tem a velocidade de rotação.
A média de retenção de pico não é tecnicamente um processo de cálculo da média. O algoritmo de deteção de pico retém o valor espectral mais elevado registado durante o tempo de cálculo da média (efetivamente o pior dos resultados). Cada vez que os dados da forma de onda forem transformados para o domínio espectral, cada linha de dados de amplitude é comparada com a anterior e a maior amplitude é mantida. Este processo é repetido até que o analista pare a recolha de dados, ou até que o número de médias programadas seja cumprido. O ruído e todos os outros sinais de fundo são todos mantidos nos valores de pico.
2.2.2 A análise por ordens
Ao analisar máquinas rotativas, os dados medidos dependerão da velocidade de rotação. As velocidades de rotação variáveis alterarão as características dos dados medidos.
Os componentes do sinal medido que mudam de frequência de acordo com as variações de velocidade são referidos como harmónicos da velocidade de rotação ou ordens.
O 1º componente harmónico tem uma frequência igual à velocidade de rotação, indicada em Hz, e por exemplo, o 10º harmónico tem uma frequência 10 vezes superior ao 1º harmónico. As variações de velocidade fazem com que os componentes relevantes da frequência harmónica mudem para cima e para baixo na frequência.
Se um sistema medido estivesse a funcionar com uma velocidade de rotação perfeitamente constante, então as ordens harmónicas nos espectros FFT manter-se-iam nas mesmas linhas espectrais durante toda a medição. Na realidade, as máquinas terão algumas variações de velocidade, mesmo que estejam definidas para funcionar a um determinado valor de rpm.
Quando se utiliza a análise de ordem em vez da análise FFT, os espectros relacionar-se-ão com as vibrações por rotação em vez das vibrações por segundo. Por conseguinte, será independente da velocidade de rotação. Isto proporciona padrões de ordem harmónicos estáveis através de velocidades variáveis para componentes de vibração relacionados com a rotação.
Outra vantagem de usar a análise de ordens para medições relacionadas com a rotação é evitar o alargamento das componentes do espetro relacionadas com a ordem. O alargamento acontece quando o padrão de frequência muda durante o cálculo de um espectro. Isto pode ser tanto durante o cálculo de um espectro instantâneo como através de múltiplos espectros instantâneos que são medidos em conjunto.
Os espectros com alargamento carecerão de picos harmónicos claros, uma vez que as frequências de pico estavam a mudar durante tais cálculos de espectro. Em vez de picos harmónicos claros, os espectros alargados espalharão a energia das ordens harmónicas pelas gamas de frequências relacionadas com todas as velocidades de rotação presentes durante o cálculo do espectro.
Ao utilizar a análise de ordem, evita-se a mancha espectral para tais sinais não estacionários, uma vez que os componentes harmónicos de rotação permanecem em posições de ordem fixa nos espectros de ordem.
Para se poder efetuar a análise por ordens é necessária informação sobre a velocidade de rotação da máquina, normalmente medida com um tacómetro.
2.2.3 Identificação de frequências naturais com um analisador de vibrações – A cascada de espetros
Na cascada de espetros estes são apresentados ao longo do tempo ou de outro parâmetro.
2.2.4 Identificação de frequências naturais com um analisador de vibrações – O Bode
O gráfico de Bode é meramente de amplitude de vibração e fase versus velocidade do veio. No entanto, pode potencialmente fornecer muita informação não disponível nas medidas em regime estacionário como o FFT. A utilização mais comum do Bode é a identificação das frequências naturais presentes nas máquinas. As mais comuns são as chamadas “velocidades críticas” que ocorrem quando a velocidade de rotação do veio coincide com uma frequência natural e produz uma ressonância. Isto aparece como um pico de amplitude e mudança de fase no gráfico do Bode. A identificação de frequências naturais é especialmente crítica nas turbomáquinas porque, ao contrário da maioria dos equipamentos de uso geral, funcionam acima ou perto de uma, se não mais, frequências naturais ou modos. O gráfico de Bode é mais poderoso na identificação de vibrações síncronas. Enquanto que a vibração global pode ser traçado também em relação à velocidade do veio, o gráfico Bode não é realmente uma ferramenta para identificar vibrações não-síncronas.
2.2.5 Identificação de frequências naturais com um analisador de vibrações – O diagrama Polar (Nyquist)
O gráfico Polar apresenta exatamente os mesmos dados que o gráfico Bode, apenas num formato de visualização diferente. Na parcela polar, a magnitude do vetor de deslocamento é medida radialmente, a partir do centro do gráfico e a fase é traçada circunferencialmente. Uma ressonância é indicada num gráfico pela velocidade a que a amplitude é a máxima de um loop (ou seja, aproximadamente 180 graus de mudança de fase).
2.3 Ensaios efetuados com a máquina em funcionamento – a média negativa
A média negativa é um método de ensaio de impacto, com a máquina em funcionamento.
Se efetuarmos impactos na máquina, quando não está em funcionamento, obtemos apenas as frequências naturais. Mas se a máquina estiver a funcionar, então obtemos também o espectro com a sua velocidade de rotação e harmónicas e outras frequências. Estes dois espectros são o que podemos ver no ecrã.
O procedimento de médias negativas elimina as frequências de funcionamento. Desta forma, apenas as frequências naturais permanecem no espectro.
Para se efetuar uma média negativa, quando se inicia a medição, em primeiro lugar, é tomado o espectro de referência, com a máquina em funcionamento. Isto significa que este espectro contém apenas as frequências de funcionamento.
Seguidamente efetuam-se repetidamente impactos na máquina. De cada espectro medido o analisador retira o espectro de referência com as frequências de funcionamento, que foi medido no início. A média é efetuada a partir destes espectros subtraídos.
Como medimos as vibrações geradas por impactos, para se obterem melhores resultados deve ser utilizada a janela exponencial, utilizando-se também, o trigger de amplitude.
3 Identificação de frequências naturais com um analisador de vibrações – Exemplo de aplicação
3.1 Identificação de frequências naturais com um analisador de vibrações – O objetivo do ensaio
Para este exemplo vamos utilizar um modelo didático que é uma esmeriladora. O objetivo do ensaio consiste em medir as frequências naturais da esmeriladora, apoiada nos seus apoios de borracha, de diferentes formas.

Como equipamento de medida vamos utilizar um analisador de vibrações multicanal ADASH VA5Pro com acelerómetros e um tacómetro.
3.2 Identificação de frequências naturais com um analisador de vibrações – Os pontos de medida e de excitação
A cada frequência natural está associada um modo de vibração.
Os modos de vibração que esperamos ver na base do modelo nos seus apoios, são os de translação e de oscilação, como se podem ver a seguir.
Os pontos de medida e excitação são escolhidos em função do modo que se quer ver.
Assim o modo de vibração de translação poderá ser excitado por um impacto no meio do modelo ou por um desequilíbrio de força como se vê na figura. O modo de oscilação poderá ser excitado por um impacto num dos extremos do modelo ou por um desequilíbrio de binário.
| Ponto de excitação para identificar o modo de vibração de translação | Ponto de excitação para identificar o modo de vibração de oscilação |
 |  |
3.3 Identificação de frequências naturais com um analisador de vibrações – Ensaios com a máquina parada
3.3.1 Ensaio de impacto
a) Ponto de excitação de força e acelerómetro de medição de resposta no centro do modelo
Os resultados deste ensaio podem ser vistos no programa DDS da ADASH. O pico mais elevado corresponde à frequência natural de translação na direção vertical.
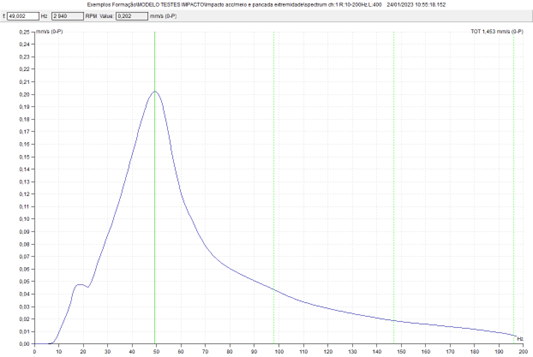
b) Ponto de excitação de força e acelerómetro de medição de resposta na ponta do modelo
No vídeo a seguir apresentado pode-se ver a implementação pratica deste ensaio.
Os resultados deste ensaio podem ser vistos no programa DDS da ADASH.
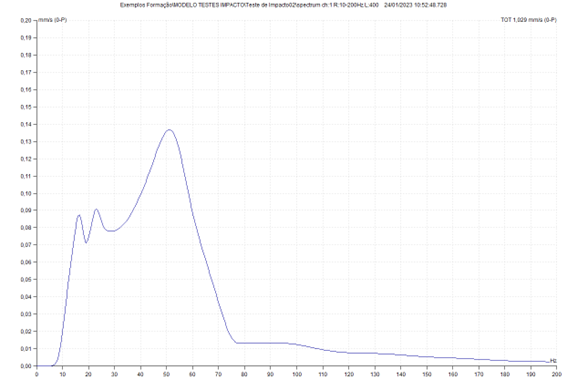
Para além da do pico mais elevado correspondente à frequência natural de translação na direção vertical, podem-se ver, a frequências mais baixas as frequências naturais dos modos de oscilação.
Da comparação desta medida com a anterior, pode-se ver a importância do ponto de excitação e de medida, para a identificação das diversas frequências naturais.
Quando a excitação é efetuada num dos nos (ponto com ausência de movimento) de um modo de vibração, este não é excitado.
3.3.2 Função de Resposta em Frequência (FRF)
No vídeo a seguir apresentado pode-se ver a implementação prática deste ensaio.
Os resultados deste ensaio podem ser vistos no programa DDS da ADASH.
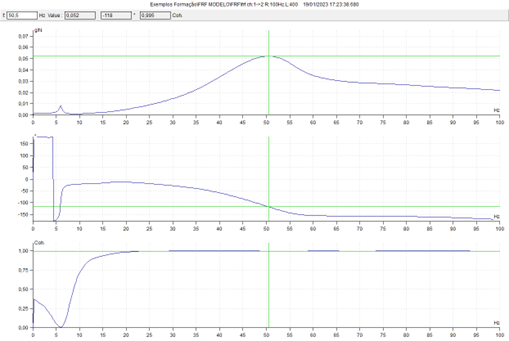
Novamente aprece a frequência natural na direção vertical na zona dos 50 KHz, como nos ensaios anteriores. Pode-se ver que consiste num pico muito largo. Isto é devido a existir um grande amortecimento devido aos apoios de borracha do modelo. A Coerência na zona desta frequência natural tem um valor próximo de 1 (0,995) indicando que está bem estimada. Vê-se também claramente a variação de fase a esta frequência.
Pode-se ver que o pico a cerca de 6 Hz, tem um valor de coerência muito baixo e, portanto, deve ser descartado; não é uma frequência natural.
3.4. Identificação de frequências naturais com um analisador de vibrações – Ensaios efetuados com a máquina em variação de velocidade
3.4.1 A média de retenção de pico (Peakhold)
No vídeo a seguir apresentado pode-se ver a implementação prática deste ensaio com o modelo com um desequilíbrio de momento que vai excitar as frequências naturais de translação e de oscilação.
Os resultados deste ensaio podem ser vistos no programa DDS da ADASH.
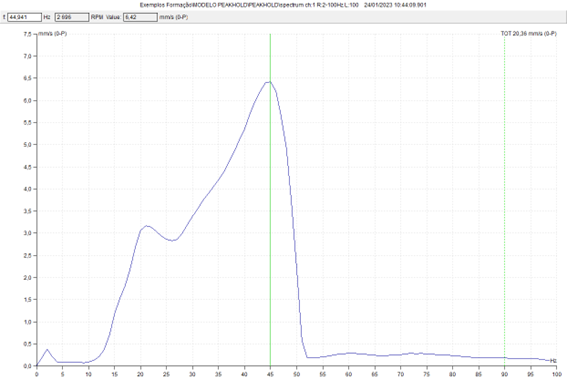
Para além da do pico mais elevado correspondente à frequência natural de translação na direção vertical, podem-se ver, a frequências mais baixas, as frequências naturais dos modos de oscilação.
3.4.2 A análise por ordens e cascada
No vídeo a seguir apresentado pode-se ver a implementação prática deste ensaio com o modelo com um desequilíbrio de força que vai excitar a frequência natural de translação. Note-se o tacómetro para permitir a análise por ordens.
Recorremos à funcionalidade do VA5PRO, que nos permite efetuar estas medidas (e mais algumas…) em paralelo e, desta forma, termos a comparação de resultados simplificada.
Na análise por ordens, independentemente da velocidade de rotação do modelo, a componente a 1xRPM é sempre apresentada na mesma posição no espetro. Note-se que a componente a 1xRPM e mais estreita no espetro de ordens que no espetro a frequência fixa.
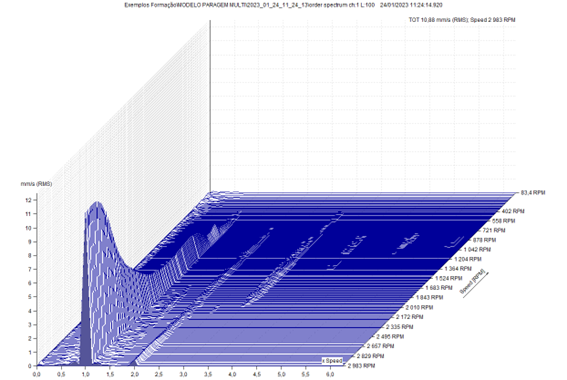
Note-se a velocidade de rotação medida, na aquisição dos sucessivos espetros, do lado direito em baixo. A componente a 1x RPM aparece sempre na mesma posição do espetro.
O gráfico a seguir apresentado foi obtido a partir de um corte no gráfico anterior a 1x RPM. Note-se a frequência natural a 48 Hz.
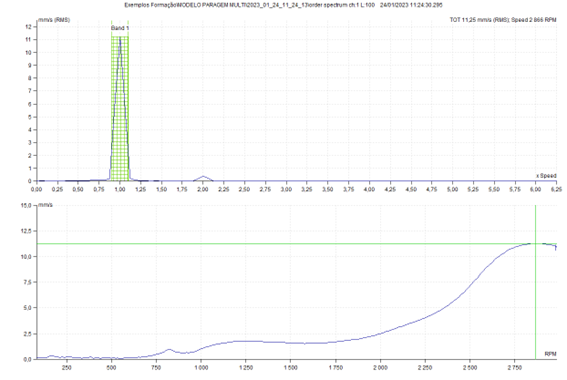
A seguir pode-se uma Cascada, para o qual não é necessário o tacómetro.
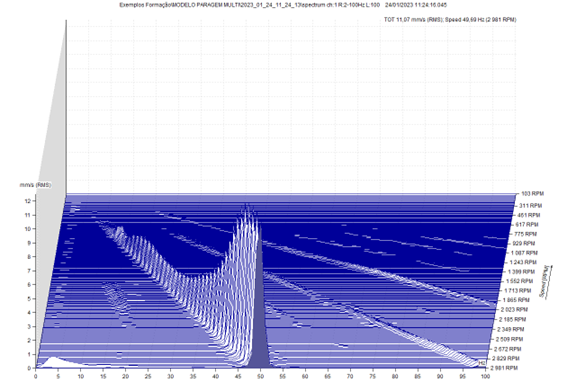
Nestes dois espetros, a seguir apresentados, o de cima obtido a frequência fixa, e o de baixo em ordens, pode-se ver que no espetro de cima, a componente à frequência de rotação, obtida a 2952 RPM, está “alargada”, devido à variação de velocidade do modelo, durante a medição, relativamente à do espetro em baixo.
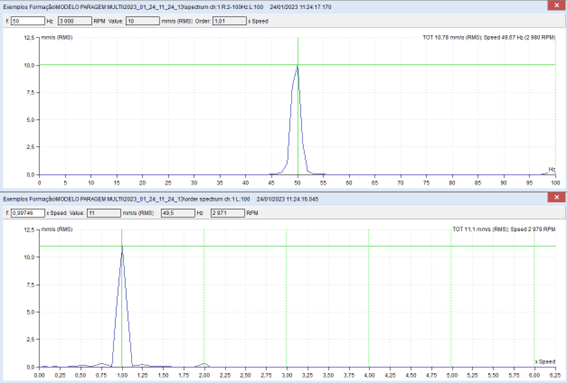
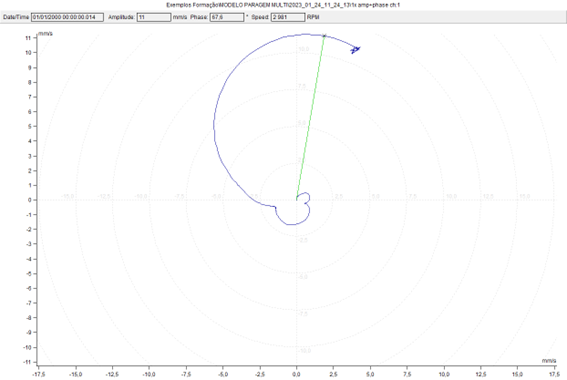
Novamente se pode ver, bem marcada, a frequência natural associada ao modo de vibração de translação na direção vertical, a 48 Hz, com muito amortecimento.
3.4.3 O Bode e o Nyquist (ou polar)
Recorrendo à funcionalidade do VA5PRO, que nos permite efetuar estas medidas (e mais algumas…) em paralelo, vamos recorrer aos dados do último ensaio para os visualizar no programa DDS da ADAH.
A seguir pode-se ver um gráfico de Bode obtido a partir da análise por ordens, durante a anterior paragem do modelo. Novamente, como seria de esperar, pode-se ver, bem marcada, a frequência natural associada ao modo de vibração de translação na direção vertical, a 48 Hz, com muito amortecimento.
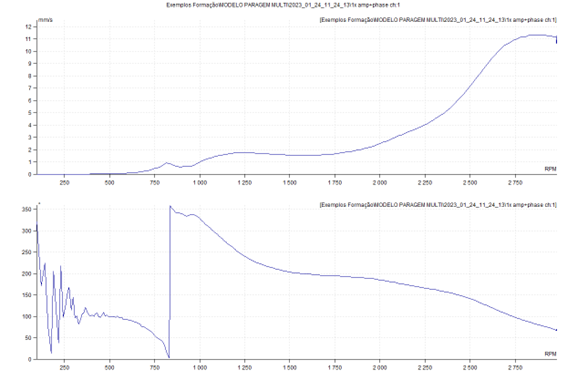
A seguir pode-se ver a o gráfico de Nyquist (ou polar) dos mesmos dados. Neste gráfico a variação de fase de 180 é mais óbvia. A ressonância ocorre quando o vetor é máximo.
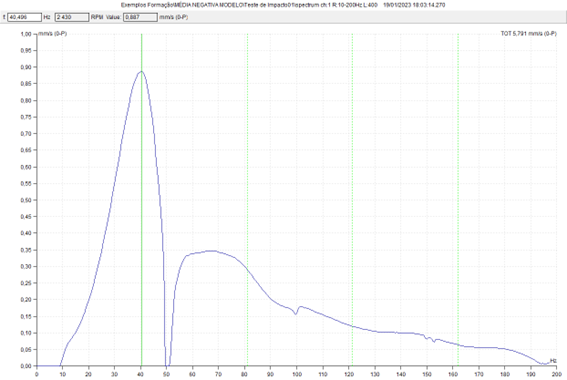
3.5. Identificação de frequências naturais com um analisador de vibrações – Ensaios efetuados com a máquina em funcionamento – a média negativa
No vídeo a seguir apresentado pode-se ver a implementação prática deste ensaio.
Os resultados deste ensaio podem ser vistos no programa DDS da ADASH.
4 Identificação de frequências naturais com um analisador de vibrações – Conclusão
Aqui foram revistas diversas técnicas que podem ser utilizadas para identificar experimentalmente frequências naturais.