Processamento de dados de vibrações
Introdução – Processamento de dados de vibrações
O processamento de dados de vibrações é o tema deste capítulo. Trata-se da configuração e das limitações da instrumentação utilizada para fazer medições de vibração de rotina. Incluídos estão os analisadores FFT (analisadores de transformadas rápida de Fourier) e coletores de dados. O analisador FFT e o coletor de dados são utilizados visualizar a forma de onda (para avaliar períodos e órbitas), na análise espectral e na avaliação da forma de onda no tempo. A forma de onda no tempo é utilizada para fazer a triagem e analisar a sua forma.
Processamento de dados de vibrações e ecrã de forma de onda (osciloscópio)
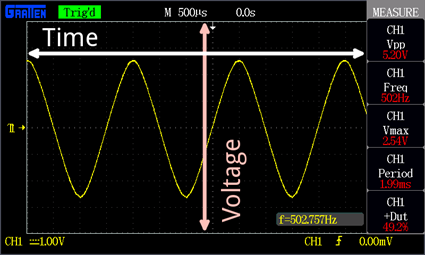
O ecrã de forma de onda mede e mostra voltagens que variam com o tempo. Um transdutor converte a vibração mecânica num sinal elétrico proporcional calibrado nas unidades de engenharia (UE) de milivolts (mv) por micrómetro (μm), milímetros por segundo (mm/s) ou g.

Os ecrãs de forma de onda são utilizados para mostrar formas de ondas no tempo, órbitas e marcadores relacionados com eventos como a rotação do veio como se vê na figura a seguir.
A função de trigger
A função de trigger (gatilho) é uma função importante tanto do osciloscópio como do analisador FFT. Um dispositivo de trigger inicia a aquisição de dados num momento ou amplitude específicos e controla a aquisição de dados através de um sinal específico (vibração ou trigger). O osciloscópio pode ser colocado em modo de trigger automático para fazer uma amostragem contínua dos dados. A função de trigger pode ser feita num sinal selecionado com base na inclinação e/ou magnitude da voltagem. O osciloscópio pode ser configurado para fazer uma única medida desencadeada numa voltagem específica. Para medições contínuas, um captador ótico ou um sensor de proximidade poderão ser utilizados como triggers contínuos, à frequência do veio.
Intensidade externa de entrada
Pode ser apresentada no ecrã do osciloscópio uma supressão controlada ou marca de intensidade, através da aplicação de um sinal de +/- 5volt ao conector do veio z. O input pode ser acoplado a AC (i.e., sem passagens DC). Se não estiver, deve ser utilizado um condensador com sensores de proximidade com mais de 5 volts DC. A supressão do veio z é utilizada para medir fase e para relacionar uma marca no veio com a vibração durante a equilibragem. O sinal de supressão é obtido a partir do trigger de um sensor de proximidade ou ótico.
Processamento de dados de vibrações e o analisador FFT
O analisador de FFT é um instrumento digital.

Conversão do sinal analógico num conjunto de amostras
Um bloco de dados digitalizado num conversor analógico-digital é processado num algoritmo de transformadas rápida de Fourier (FFT) para produzir um espectro.

A forma de onda no tempo é reconstruída a partir do bloco de dados digitalizado. Um analisador de FFT de dois canais permite obter as propriedades de e fase entre dois sinais obtidos. O analisador, de FFT, tem uma alta resolução, mas pode comprometer a precisão da amplitude, dependendo da sua configuração. É basicamente um analisador para utilizar em estados estacionários ao invés de dados transitórios.
O analisador recolhe um bloco de dados a uma taxa de amostragem elevada– ex.: superior a 200000 amostras por segundo – dependendo do maior intervalo de frequência do analisador. O analisador requer que um bloco completo de um ciclo inteiro antes de processar quaisquer dados pela FFT.
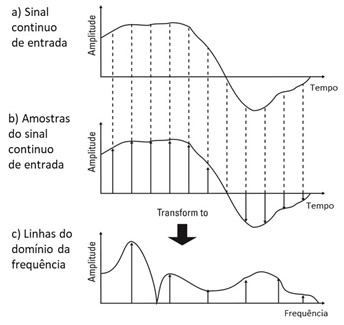
Isto significa que, para baixas frequências (menos de 10 Hz), são necessários longos tempos de amostragem antes do início do processamento do FFT. A capacidade do analisador de monitorizar eventos quando a velocidade está a mudar rapidamente é, portanto, comprometida.
Às frequências comuns em máquinas, o tempo de cálculo para o processamento da FFT, é uma fração do tempo de aquisição de dados e de variação automática de tempo.
Para saber mais sobre este tema clique aqui.
O zoom
A função de zoom no analisador de FFT aumenta a resolução; são utilizadas 400 ou 800 linhas, mas o intervalo de frequência é diminuído para uma frequência definida (início ou centro) de forma a atingir uma resolução de frequência. A resolução refere-se à capacidade do instrumento de permitir ver frequências situadas muito juntas no espectro.
Os analisadores de FFT têm janelas para preparar os dados digitalizados para o processo de FFT. O intervalo dinâmico de analisadores de FFT é, atualmente, próximo de 120dB (24 bits). Portanto, um sinal com um milivolt pode ser resolvido na presença de um sinal de dois volts. As muitas outras funcionalidades de analisadores de FFT incluem órbitas, curvas de Bodé, gráficos polares, diagramas em cascata, e gráficos reais e imaginários utilizados para análise modal.
Processamento de dados de vibrações e o coletor de dados
O coletor de dados, que hoje em dia também é um analisador FFT, recolhe e armazena parâmetros de vibração selecionados, como a vibração global, vibração total em bandas de frequência selecionadas, espectros, formas de ondas no tempo, órbitas, diagramas em cascata, medidas de alta frequência e espectros de envelope.
Numa rotina de inspeção pré-estabelecida o nível global de vibrações é normalmente armazenado como velocidade de vibração, em pico ou rms, e relacionado com pontos de medida, que podem incluir muitas máquinas.
Os dados são transferidos para computador, para os comparar com informação previamente adquirida, para que, quaisquer mudanças nas condições da máquina, possam ser identificadas.
Os algoritmos FFT foram introduzidos nos coletores e, após várias gerações, muitos são agora respeitáveis analisadores FFT com uma resolução e alcance dinâmico adequados. Alguns coletores têm capacidade para mais de 6400 linhas. Obviamente, o tempo de aquisição de dados aumenta 16 vezes mais que o de um espectro de 400 linhas.
Os números de linhas tipicamente disponíveis são 100, 200, 400, 800, 1600, 3200 e 6400. O número elevado de linhas fornece uma ampliação válida, mas é necessária uma expansão para ver dados muito próximos no ecrã do computador.
Processamento de dados de vibrações e Nº de amostras no bloco de tempo e nº de linhas no espetro
O sinal de entrada de um transdutor é digitalizado antes do processamento por FFT, como mostra a figura. O número de amostras armazenadas na memoria de entrada (buffers) dos analisadores depende do número de linhas selecionado para o espetro. A memória de entrada regista estes valores como componentes Y (amplitude) e X (tempo) igualmente espaçados.
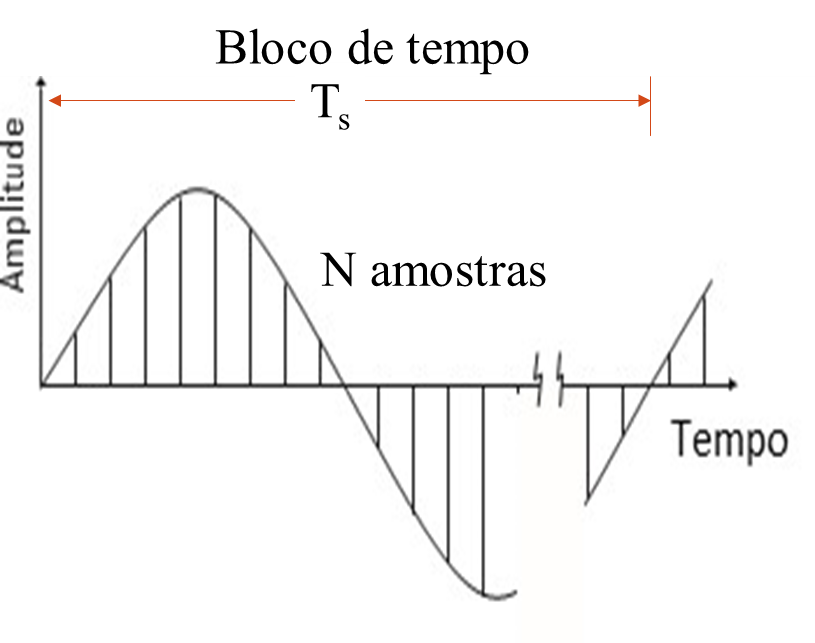
Não pode ser identificada nenhuma frequência menor que 1/Ts, porque a informação no buffer do analisador estaria incompleta.
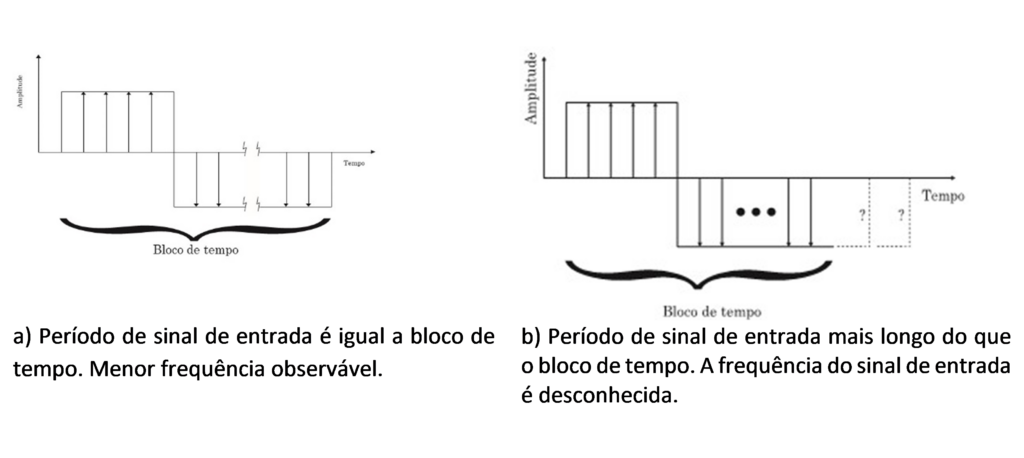
A seguir mostra-se a relação entre o número de amostras do bloco de tempo e o número de linhas do espetro.
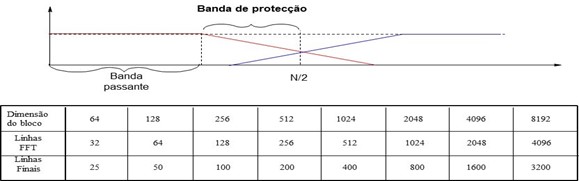
A figura a seguir mostra o resultado da transformação das amostras da forma de onda, igualmente espaçadas, num espectro de 100 linhas ou bins. Estas bins igualmente espaçados começam na menor frequência resolúvel, que é um dividido pelo tempo de amostragem, ou seja, 1/Ts. Neste caso, como se tem uma grama de frequência de 100 Hz, e o número de linhas é de 100, tem-se uma resolução de 1 Hz. O inverso de 1 Hz é um segundo que corresponde ao tempo de aquisição de um bloco de tempo para se calcular o FFT e obter este espetro.
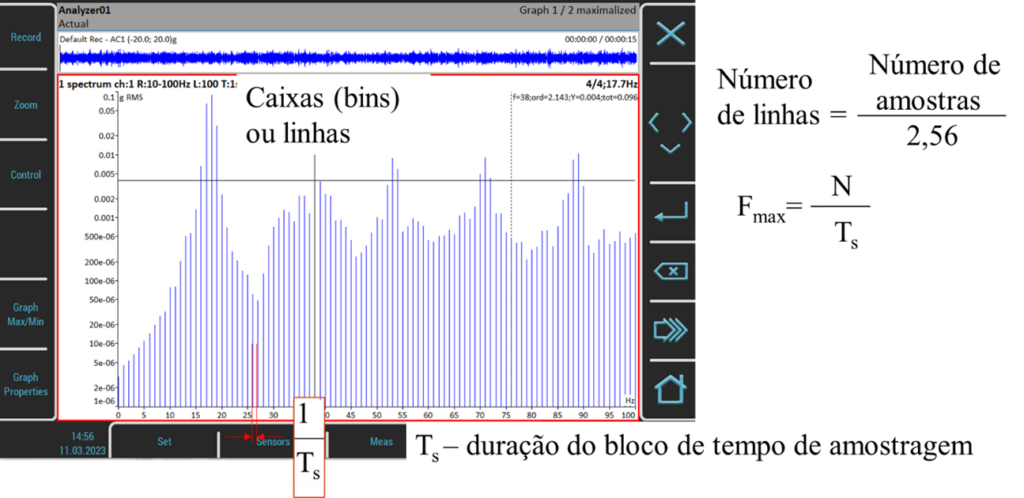
O espectro pode ter N bins (linhas) – normalmente de 100 a 6400, dependendo do número de amostras recolhidas pelo analisador ou coletor de dados. O número de amostras do bloco de tempo é 1024, caso se pretendam 400 linhas no espetro.
Para ajustar o número de amostras recolhidas ao longo do tempo de aquisição de dados é usada a filtragem digital. O número de amostras do bloco de tempo está, portanto, relacionado com o número de linhas selecionado para o espetro, por um fator de 2,56.
A taxa de amostragem de dados no tempo, é ajustada pelo analisador, para obter o número de amostras necessário ao longo da duração do tempo de recolha dos dados selecionados (N/Fmax).
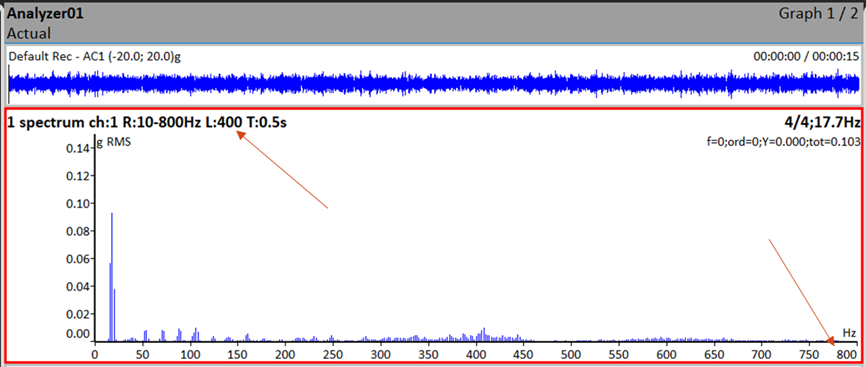
A fórmula para a frequência máxima e tempo de aquisição de dados é Fmax = N/tempo de recolha de dados. O valor de Fmax é colocado no analisador, e o ecrã do tempo automaticamente tem o período adequado, como se vê na figura a seguir.
Por exemplo, se o valor de Fmax é 800 Hz; e o número de linhas é 400, tem-se que, o tempo de recolha de dados deve ser Ts = N/Fmax = 400/800, ou 0,5 segundos. Esta relação estabelece o intervalo de tempo necessário para recolher os dados, independentemente da velocidade do equipamento de medida.
Processamento de dados de vibrações e Aliasing
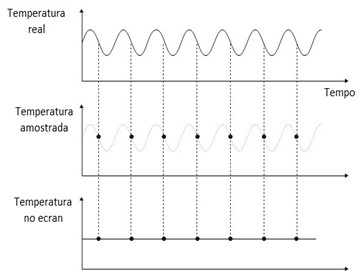
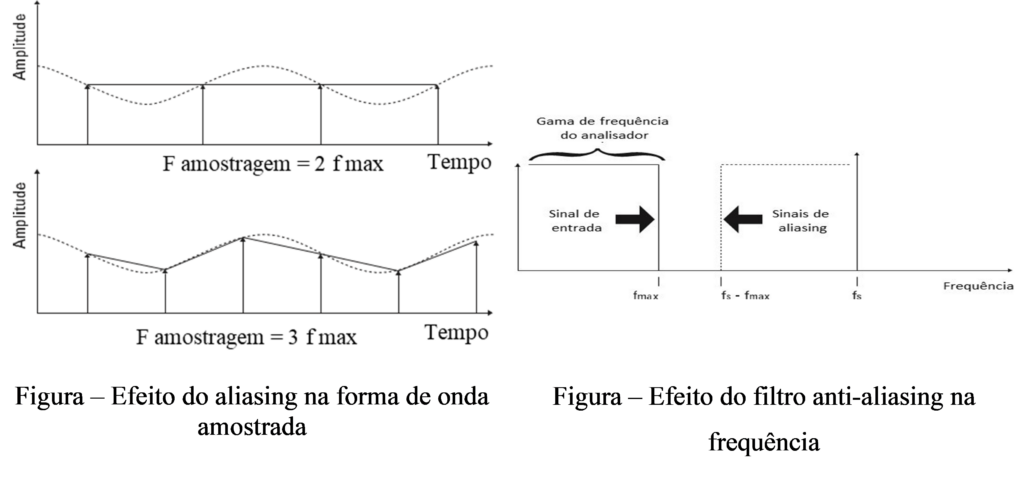
A amostragem da forma de onda com uma taxa insuficiente que se ilustra na figura resulta em dados perdidos e causa frequências falsas devido ao aliasing. Este fenómeno ocorre no espectro, se a taxa de amostragem for menor que as frequências presentes nos dados.
A na figura a seguir (topo) mostra uma amostragem de dados na mesma frequência que uma temperatura varia. Os dados digitalizados resultantes seriam uma linha reta. Frequências falsas ou aliased são obtidas no espectro quando a frequência de amostragem é menor que a maior frequência presente nos dados.
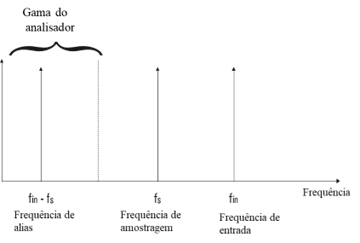
Portanto, há que ter cuidado com algoritmos FFT que não têm filtros anti-aliasing. O Critério de Nyquist diz que a taxa de amostragem de um analisador deve ser maior que duas vezes a maior frequência presente. Atualmente, os equipamentos fornecidos como analisadores de frequência, tem todos filtros deste tipo, de forma que os seus utilizadores não se tenham de preocupar com isto.
A figura a seguir ilustra o efeito de uma frequência de amostragem de duas e três vezes a frequência máxima. O filtro anti-aliasing é um filtro passa-baixo que elimina frequências nos dados que são suficientemente altas para causar aliasing.
No vídeo a seguir apresentado, vê-se um exemplo de aliasing. A frequência da imagem filmada é quase igual à velocidade de rotação do rotor do helicóptero e portanto o hélice parece estar quase parado. A pequena velocidade de rotação que se vê é igual a diferença entre a frequência de filmagem e a frequência de rotação aliasing.
As janelas (Windowing) e as fugas no FFT (leakage)
O algoritmo FFT que transforma a amostra da memória de entrada – forma de onda no tempo digitalizada – num espectro, assume que os dados antes e depois da amostra são semelhantes. Por esta razão, o algoritmo FFT precisa que os dados da amostra comecem e terminem na amplitude zero como se vê na figura.
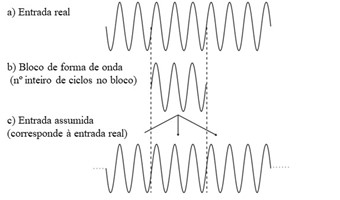
Note-se que a forma de onda reconstruída é a mesma que era antes da amostragem.
Na figura que se vê a seguir não ocorreu amostragem na amplitude zero, e é obtida uma forma de onda reconstruída que não é igual à dos dados originais. Esta forma de onda irá causar erros no espectro chamados fugas (leakage) – isto é, a energia que existe numa linha do espetro é dispersa por outras adjacentes.
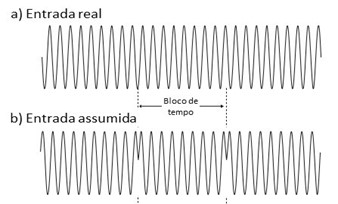
O espectro resultante, mostrado na figura a seguir, implica perda de resolução.
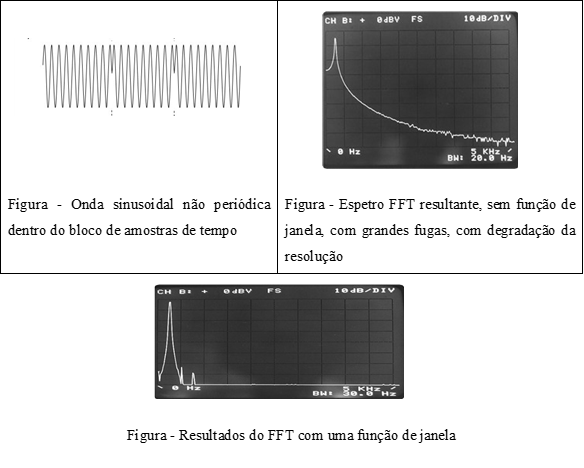
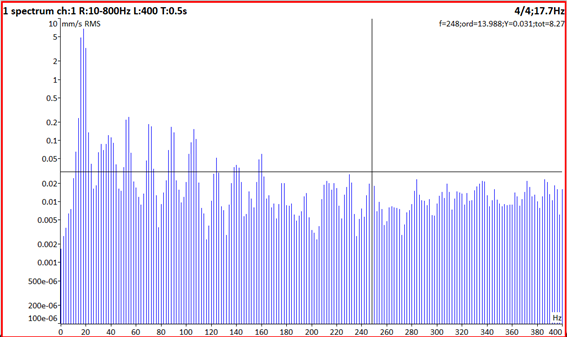
Note a resolução espectral por volta de 1 Hz, num espetro em coordenadas verticais logarítmicas, de um analisador de vibrações. Veja-se que a energia na componente a 17 Hz, corresponde à velocidade de rotação, se dispersa em diversas linhas.
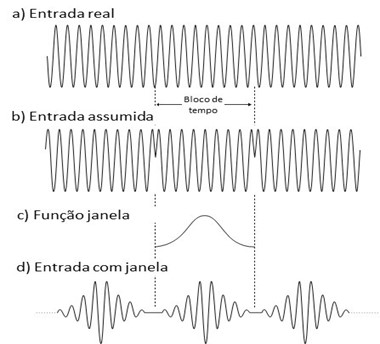
Como a aquisição de dados não pode ser controlada para obter uma amostragem periódica, são utilizadas janelas para forçar os pontos finais dos dados para zero, como se pode ver na figura.
Processamento de dados de vibrações e as janelas “Hanning” e “Uniforme”
Uma função das janelas é multiplicada por cada bloco de sinal de forma a obter um registo que é zero em ambos extremos. Não são necessárias e não devem ser utilizadas janelas quando os dados transitórios obtidos começam e acabam em zero. Uma janela Hanning destrói parte dos dados num sinal transitório porque dados importantes no início de uma amostragem podem ser eliminados como se vê na Figura.
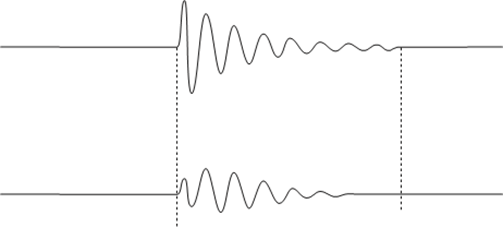
Para resposta de dados transitórios pode ser utilizada uma janela “Uniforme”. A janela Hanning tem um filtro limitado dentro da caixa ou linha que permite uma largura de banda com boa resolução como se vê na figura.
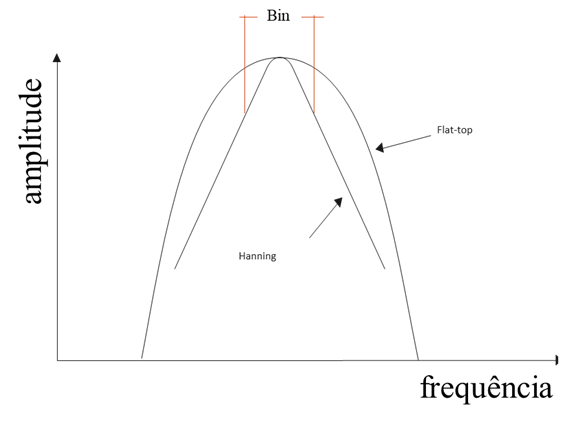
No entanto, como é limitada dentro da caixa, a imprecisão da amplitude (por vezes chamada de imprecisão de largura de banda) pode ter o valor de 1.5 dB (16%) se a frequência medida cair no bordo da caixa como se vê na figura a seguir.
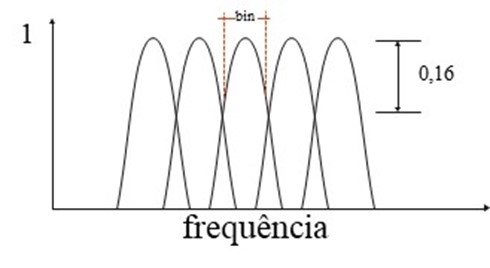
A janela flat-top tem menor resolução, mas tem apenas uma imprecisão de amplitude de 0.1 dB (1%). Portanto, a janela flat-top é recomendada para linhas espectrais discretas e precisão de amplitude. A janela Hanning é recomendada para dados estáveis com múltiplas frequências. A resolução atual para cada janela pode ser calculada utilizando o fator de janela fornecido na Tabela a seguir apresentada.
Tabela – Seleção de janela FFT
| Janela | Objetivo | Incerteza de amplitude | Fator de janela (WF) |
| Uniforme | Testes de impacto | 56.5% | 1 |
| Hanning | Análise de avarias | 16% | 1.5 |
| Flat top | Avaliação da condição | 1% | 3.8 |
Resolução = 2x largura de banda da linha = 2 x Fmax x (WF)/ número de linhas
A resolução de confiança do analisador é duas vezes a gama da frequência do espetro, multiplicado pelo fator de janela, dividido pelo número de linhas selecionado.
As janelas uniformes ou retangulares são utilizadas em testes de impacto, a menos que os dados não cheguem a zero dentro da amostra. Por esta razão, batidas duplas dentro do tempo de aquisição de dados, tem de ser evitadas.
Para saber mais sobre este tema clique aqui.
Processamento de dados de vibrações Gama Dinâmica e “autorange”
A gama dinâmica refere-se à capacidade de um analisador identificar componentes de baixa amplitude, na presença de componentes de elevada amplitude, no espectro.
A gama dinâmica determina se as amplitudes a diferentes frequências podem ou não ser determinadas. Atualmente a maioria dos equipamentos tem 120 dB (24 bit) de gama dinâmica. Antigamente a maioria dos coletores de dados, (16 bit) tinham 90 dB de gama dinâmica. Para estes equipamentos, um bit é usado para o sinal +/- (assim, 215 = 32,768). Isto significa que sinais AC com uma diferença em amplitude até 32,000 para 1 podiam ser determinados (sinais DC de 64,000 para 1). Coletores de dados mais antigos de 12-bit tinham uma gama dinâmica de 66 dB (2048-1). Antigamente, se a gama de entrada do analisador FFT estivesse regulada muito alta para a diferença de amplitudes dos dois sinais, a gama dinâmica não seria suficiente para permitir observar a amplitude de sinal mais baixa.

Atualmente, com 120 dB de gama dinâmica, os equipamentos já não necessitam de mais nenhuma regulação de escala.
Processamento de dados de vibrações – Escalas lineares e logarítmicas
Na análise da vibração ocorrem problemas quando a aceleração ou deslocamento são exibidos num espectro, com um grande intervalo de frequências, e os seus componentes são mostrados a frequências altas e baixas. Obtém-se uma ampla gama dinâmica utilizando uma escala de amplitude logarítmica, que são escalas comprimidas.
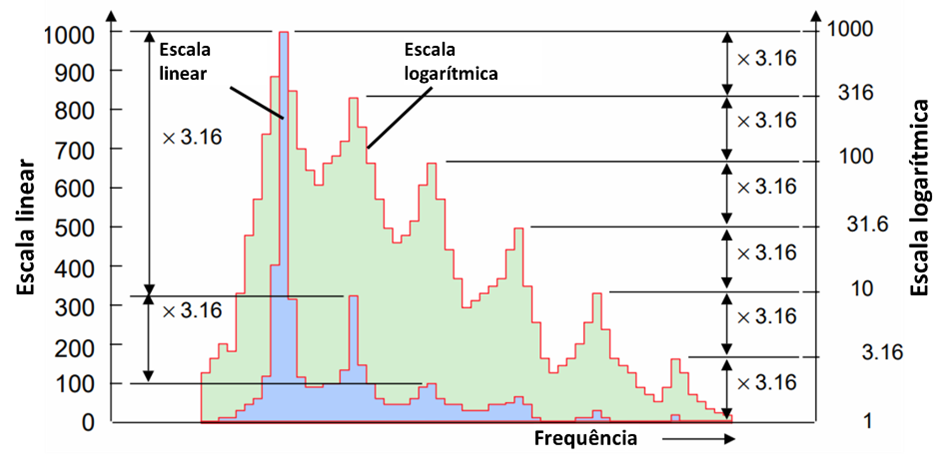
A figura anterior mostra ambas as escalas, a linear e a logarítmica. Uma segunda ordem que é apenas 0.1% (1/1000) do valor da primeira ordem, não aparecerá na escala linear, mas aparecerá a menos 60 dB que a primeira ordem na escala logarítmica.
dB = 20 log V/Vref, ou dB = 20 log 1/1000 = -60
Esta situação pode ocorrer na fase inicial da avaria de rolamentos e as amplitudes estão contidas num espectro com significativas amplitudes de vibração das engrenagens. Um exemplo é 17,4 mm/s a frequência de engrenamento e 0,25 mm/s a frequência de defeitos de rolamentos. A gama dinâmica requerida seria:
dB = 20 log 17,5/0,25 = 36,9 dB
Esta gama dinâmica está disponível em todos os coletores de dados modernos; contudo, a gama dinâmica deve ser adequadamente configurada no analisador, ou deverá ser usada a função de autoescala (autorange).
É importante dispor de uma boa gama dinâmica quando se pretende medir acelerações de baixa frequência ou deslocamentos de alta frequência na presença de uns com baixas frequências.
Os analisadores modernos, com conversores analógicos digitais de 24 bit e gama dinâmica de 120 dB já não necessitam da função autorange.
Para saber mais sobre este tema clique aqui.
Processamento de dados de vibrações e – as médias
O analisador FFT pode ser usado para cálculo do valor médio para além apresentação do FFT instantâneo, após os dados serem recolhidos. Estes modos para cálculo do valor médio, incluem rms, retenção de pico, tempo síncrono, e a sobreposição.
Para saber mais sobre este tema clique aqui.
A média rms
A média de amplitude rms é obtida pelo cálculo da média nos bins à medida que cada bloco de dados é processado. O ruído é suavizado, mas não eliminado, e os sinais discretos são reforçados no ecrã.
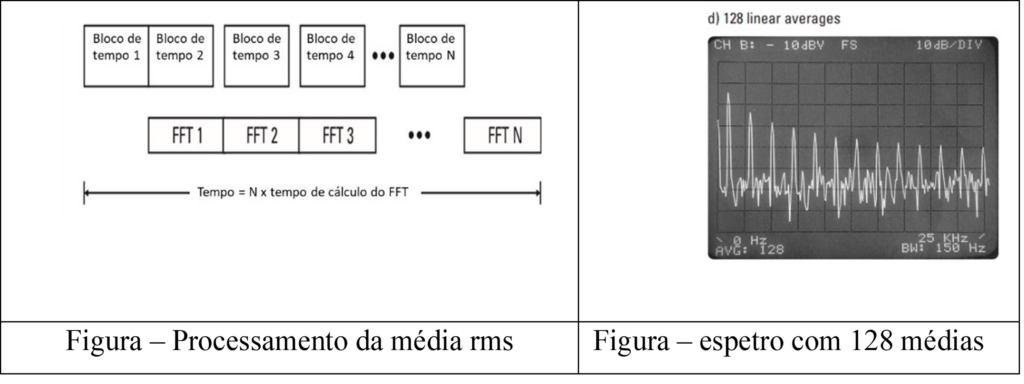
A média síncrona no tempo
A média síncrona no tempo é realizada na forma de onda. Um trigger é disponibilizado ao analisador à frequência do veio a partir de um sensor de proximidade ou de um captador ótico.
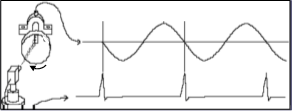
Esta técnica consiste na realização de medições da forma de onda, sincronizadas com a rotação de um dos veios e execução de uma média dessas medidas. Como resultado desta sincronização os eventos assíncronos com a realização da média, tendem para zero, enquanto os síncronos se tornam mais visíveis. Portanto, a parte periódica da entrada será sempre exatamente a mesma em cada bloco de tempo que tomamos, enquanto o ruído, é claro, variará. Se juntarmos uma série desses blocos de tempo acionados pelo tacómetro e dividir pelo número de blocos que tomamos, vamos calcular o que chamamos de média síncrona no domínio do tempo. Com esta técnica conseguimos eliminar da forma de ondas as vibrações que não estão relacionadas com o veio onde está o tacómetro.
Por exemplo, a figura a seguir apresentada mostra o resultado da aplicação da média síncrona no tempo para separar a vibração de dois rolos de prensa de máquinas de papel.
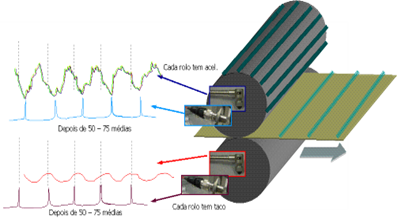
A média síncrona no tempo elemina o ruido não síncrono no sinal.
A média de retenção de pico
A função de retenção de pico, retém o maior valor de pico ou rms em cada bin à medida que cada bloco de dados novo é processado. Portanto, não faz, realmente, qualquer cálculo da média. A função de retenção de pico é usada para testes de transitórios. A maior desvantagem no uso de analisadores FFT em testes de transitórios é o longo tempo de aquisição requerido. Um bloco de dados deve ser processado antes de ser mostrado. Portanto, num teste de desaceleração, a máquina pode experimentar uma ampla alteração nas RPM enquanto uma amostra de dados está a ser recolhida. Cada retenção de pico do FFT associa apenas um ponto na curva. São precisos numerosos pontos para descrever a gama em torno da velocidade crítica.
Figura – A média de retenção de pico é utilizada para seguir a amplitude do maior pico de vibrações no espetro, durante a paragem de uma máquina e também para indicar variações de velocidade ao longo do tempo
A média exponencial
Quando se pretende ver em tempo real, uma vibração com muito ruído, ou a variar, utiliza-se a média exponencial. Na média exponencial, os blocos de tempo não contribuem para a média de forma igual. De facto, um registo novo pesa mais do que os antigos. O valor em qualquer ponto da média exponencial é dado por: y [n] = y [n-1 * (1 – α) + x [n] * α onde:
- Em primeiro lugar, n é a enésima média e o enésimo novo bloco de tempo.
- Seguidamente, alfa é o coeficiente de ponderação.
- Normalmente, alfa é definido como 1 / (Número de médias).
Por exemplo, no analisador, se o número de médias for definido como 3 e o tipo de média for selecionado como média exponencial, então α = 1/3. A vantagem deste tipo de média é que pode ser usada sem fim. Ao contrário da média RMS, a média exponencial não parará ao fim de n vezes. Como foi referido, a média RMS termina ao fim de algum número de médias. Pelo contrário, este tipo de média fica a ser executada até a mandarmos parar. Desta forma, o resultado da média muda à medida que adquirimos novos registos e gradualmente ignorará os efeitos dos registos antigos.
Média negativa
Processamento em sobreposição (overlap)
No processamento sobreposto, apenas uma fração dos novos dados, são recolhidos no buffer de entrada. Os dados da amostra anterior são usados para fazer uma amostra completa para processamento. O número de linhas ou bins, intervalo de frequência, e processamento sobreposto são considerações a ter em conta quando o analisador é configurado para teste de transitórios porque eles determinam o tempo de aquisição.
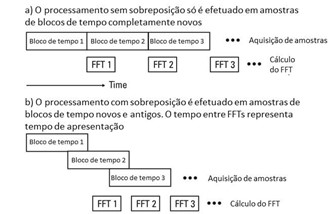
Para saber mais sobre este tema clique aqui.
Processamento de dados de vibrações – A análise do envelope
A análise do envelope é, atualmente, a ferramenta por excelência, para deteção de impactos como sejam por exemplo os gerados nas avarias em rolamentos com um analisador de vibrações. Tornou-se também essencial para diagnosticar todos os problemas mecânicos que podem gerar impactos, como sejam engrenagens em mau estado, folgas, desapertos, etc.
Originalmente, quando foi desenvolvida não tinha a capacidade de medir, com precisão, o nível da aceleração gerada pelos impactos mecânicos, mas, desde os anos noventa, com o desenvolvimento da tecnologia de deteção de picos de impacto, essa limitação foi ultrapassada.
A análise de vibrações com envelope tem tido diversas designações técnicas e comercias, nomeadamente:
- PeakVue (Emerson/CSI);
- Espectro de Spike Energy (IRD/ENTEK/Rockwell Automation);
- Desmodulação;
- Envelope;
- Etc.
No entanto apesar das diversas designações e forma de implementação, continuam todas a constituir versões de análise do envelope.
A análise do envelope – o espetro de frequência das formas de onda geradas por impactos
Referiu-se muitas vezes a representação no espetro de frequência de uma vibração sinusoidal. Quando se trata das vibrações geradas por impactos, de muito curta duração, a vibração não é do tipo sinusoidal e levantam-se novos desafios.
Na figura a seguir apresentada podem-se ver diversos tipos de forma de onda e respetivos espetros de frequência como medido por um analisador de vibrações.
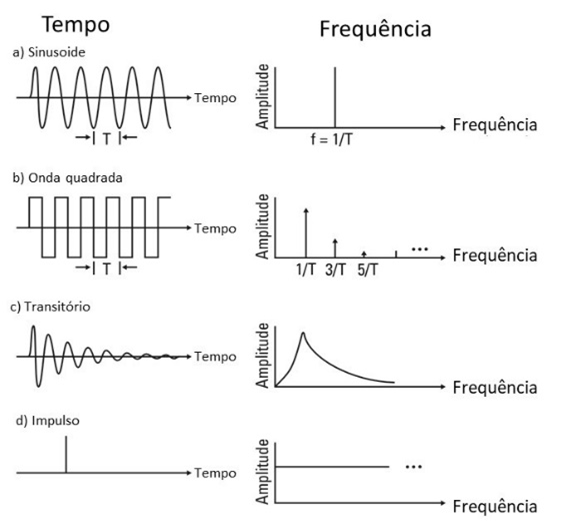
Figura – Formas de onda e respetivo espetro
O espetro de frequência de um impulso, semelhante ao gerado por um impacto, é uma linha plana, de baixa amplitude que se espalha por todas as frequências.
A análise do envelope – a medição das vibrações geradas por impactos
Existem dois desafios técnicos na medição das vibrações geradas por impactos:
- Separar as vibrações geradas por impactos, de muito baixo nível, das outras vibrações geradas numa máquina;
- Quantificar, com precisão, o nível das vibrações geradas por impactos.
A análise do envelope – a separação as vibrações geradas por impactos de muito baixo nível
Quando se trata da medição de vibrações numa máquina é frequente estarmos interessados na deteção de impactos de muito baixo nível na presença de outras vibrações de amplitude elevada existente numa máquina. É esta a situação que se enfrenta quando se tenta detetar os primeiros sintomas de avarias num rolamento.
Caso se consiga separar as vibrações dos impactos das outras vibrações existentes na máquina será muto mais simples seguir o seu crescimento, como se pode ver na figura.
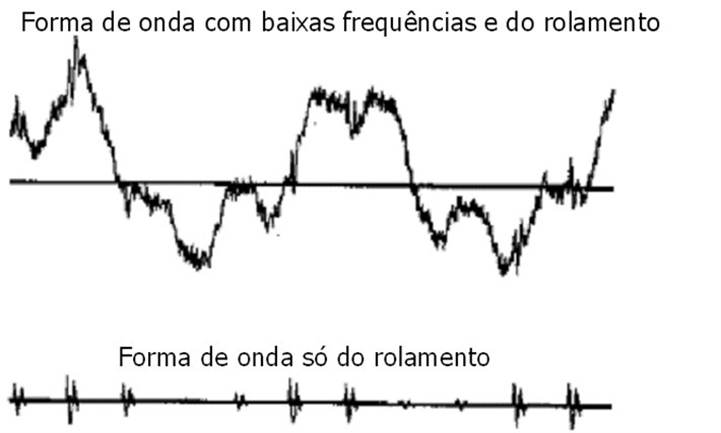
Figura A necessidade de separar as vibrações dos impactos das outras vibrações nas máquinas
Na figura a seguir apresentada vê-se no espetro de frequência as vibrações geradas pelos pequenos impactos da primeira fase de avarias em rolamentos.
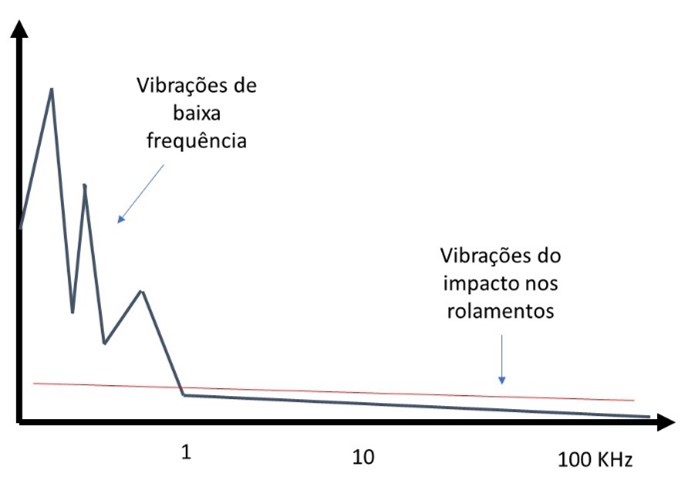
Como as vibrações dos rolamentos em degradação, nas suas fases iniciais, surgem sobretudo em aceleração, nas altas frequências, consegue-se fazer a separação/realce das vibrações dos impactos, através da utilização de um filtro passa alto das vibrações medidas. Destra forma consegue-se efetuar a separação das vibrações dos impactos rolamentos das outras vibrações da máquina.
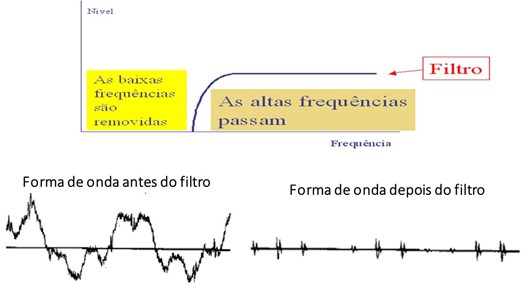
Figura Eliminação de vibração a baixas frequências – introdução de filtro passa alto
Esta filtragem é a primeira operação da análise de vibrações com envelope.
A análise do envelope – a quantificação do nível das vibrações geradas por impactos
Já foi referido o fenómeno do “aliasing” e da taxa de amostragem necessária para medir, com precisão, o nível de uma sinusoide no espetro de frequência.
Imagine-se agora que para se ver as frequências características de um rolamento se pretende ver um espetro até 1 KHz. Como se viu atrás a taxa de amostragem da forma de onda será 2,56 vezes o Fmax do espetro ou seja 2,56 KHz. Os seja o intervalo de tempo entre cada amostra é de 1/ 2560 segundos ou seja 0,4 mseg. Se a duração do impacto for inferior a este tempo, o nível do impacto não será adequadamente medido, como pode ser visto na figura a seguir apresentada.
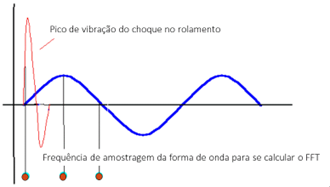
Tem-se assim que a relação fixa entre amostragem no tempo e gama de frequência, intrínseca da função matemática transformada de Fourier, com que se obtém o espetro FFT, impede que se obtenha simultaneamente:
- Uma amostragem elevada que nos permita medir adequadamente os níveis dos picos de impacto;
- Uma elevada resolução no espetro de frequência que permita identificar claramente as frequências características de defeitos em rolamentos.
A solução para esta questão consiste em tornar independente a taxa de amostragem da forma de onda para deteção de picos de impacto da taxa de amostragem para a obtenção do espectro FFT. Esta e a solução que hoje em dia é implementada por alguns fabricantes de analisadores.
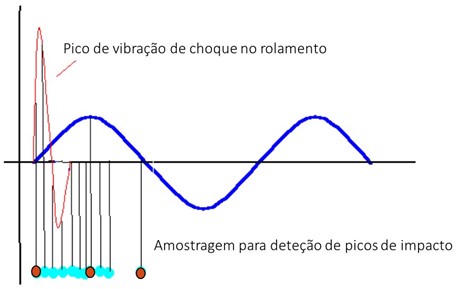
Figura Taxa de amostragem da forma de onda adequada para se caracterizar o nível de vibração gerado por um impacto
Como se vê na figura a taxa de amostragem, adequada para se caracterizar o nível de vibrações gerada por impactos é muito maior que a necessária para caracterizar o nível de uma vibração sinusoidal.
A análise do envelope – a caracterização da taxa de repetição de impactos
Para se conhecer o período de repetição dos choques a análise do envelope retifica a forma de onda antes de se efetuar o espetro FFT.
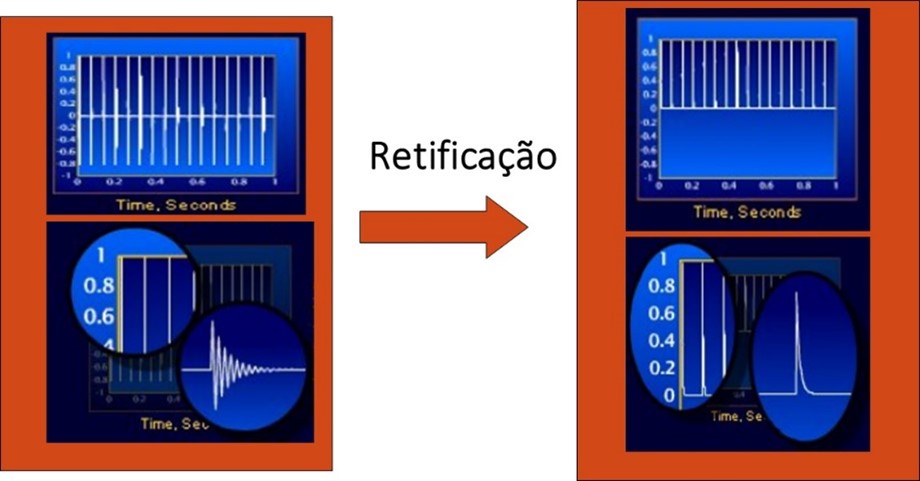
A análise do envelope – A obtenção do espetro de frequência do envelope tradicional
A análise em frequência das vibrações é efetuada na forma de onda retificada, tendo-se assim o seguinte diagrama de blocos da análise de vibrações com envelope.
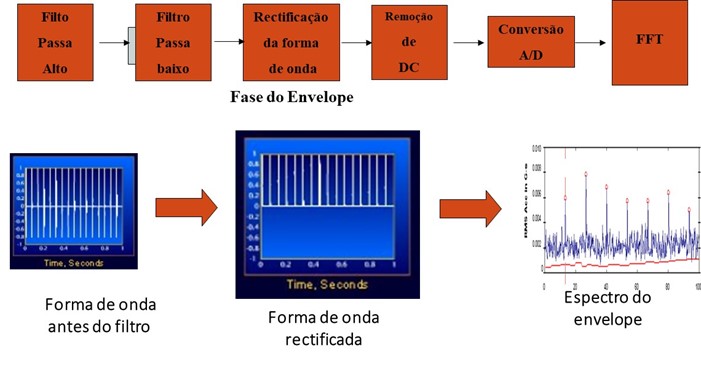
Figura – Esquema da implementação da análise de vibrações com envelope tradicional
Esta forma de implementação do espetro FFT não caracteriza adequadamente o nível das componentes da forma de onda retificada e do espetro de frequência.
O mapa espetral ou cascada
Alguns analisadores FFT geram um diagrama em cascata como se vê na figura a seguir. Este diagrama contém um certo número de espectros tomados a várias velocidades ou tempos e, nalguns casos, espaço (isto é, o analisador empilha os espectros num gráfico em cascata por posição de medição).
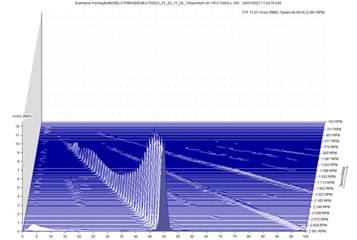
Figura Diagrama em cascata ou mapa espetral
Processamento de dados de vibrações – A análise por ordens
Ao analisar máquinas rotativas, os dados medidos dependerão da velocidade de rotação. As velocidades de rotação variáveis alterarão as características dos dados medidos.
Os componentes do sinal medido que mudam de frequência de acordo com as variações de velocidade, são referidos como harmónicos da velocidade de rotação ou ordens.
O 1º componente harmónico tem uma frequência igual à velocidade de rotação, indicada em Hz, e por exemplo, o 10º harmónico tem uma frequência 10 vezes superior ao 1º harmónico. As variações de velocidade fazem com que os componentes relevantes da frequência harmónica mudem para cima e para baixo na frequência.
Se máquina estiver a funcionar com uma velocidade de rotação perfeitamente constante, então as ordens harmónicas nos espectros FFT manter-se-iam nas mesmas linhas espectrais durante toda a medição. Na realidade, muitas máquinas terão algumas variações de velocidade, mesmo que estejam definidas para funcionar a um determinado valor de rpm.
Quando se utiliza a análise de ordem em vez da análise FFT, os espectros relacionar-se-ão com as vibrações por rotação em vez das vibrações por segundo. Por conseguinte, será independente da velocidade de rotação. Isto proporciona padrões de ordem harmónicos estáveis através de velocidades variáveis para componentes de vibração relacionados com a rotação.
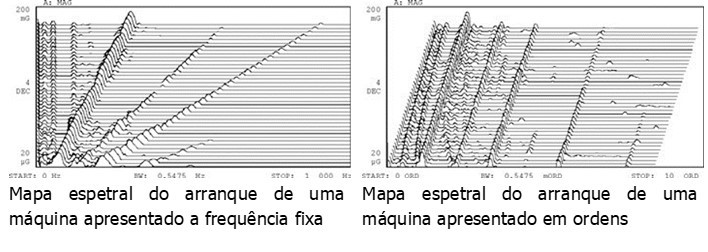
Outra vantagem de usar a análise de ordens para medições relacionadas com a rotação é evitar o alargamento das componentes do espetro relacionadas com a ordem. O alargamento acontece quando o padrão de frequência muda durante o cálculo de um espectro. Isto pode ser tanto durante o cálculo de um espectro instantâneo como através de múltiplos espectros instantâneos que são medidos em conjunto.
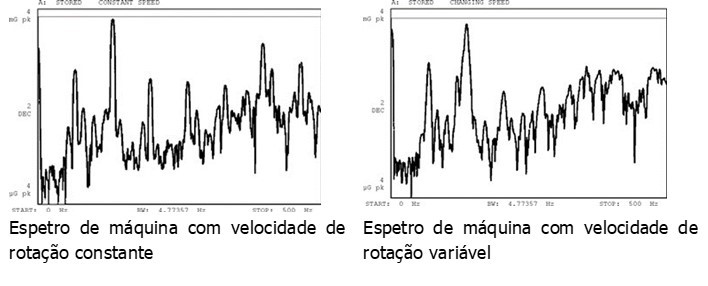
Os espectros com alargamento carecerão de picos harmónicos claros, uma vez que as frequências de pico estavam a mudar durante tais cálculos de espectro. Em vez de picos harmónicos claros, os espectros alargados espalharão a energia das ordens harmónicas pelas gamas de frequências relacionadas com todas as velocidades de rotação presentes durante o cálculo do espectro.
Ao utilizar a análise de ordem, evita-se a mancha espectral para tais sinais não estacionários, uma vez que os componentes harmónicos de rotação permanecem em posições de ordem fixa nos espectros de ordem.
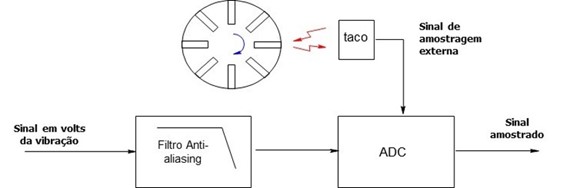
Para se poder efetuar a análise por ordens é necessária informação sobre a velocidade de rotação da máquina, normalmente medida com um tacómetro.
Processamento de dados de vibrações – O gráfico de Bodé
O gráfico de Bodé consiste na apresentação de amplitude de vibração (normalmente a 1xRPM) e fase versus velocidade do veio. Este gráfico, pode potencialmente fornecer muita informação não disponível nas medidas em regime estacionário como o FFT. A utilização mais comum do Bodé é a identificação das frequências naturais presentes nas máquinas. As mais comuns são as chamadas “velocidades críticas” que ocorrem quando a velocidade de rotação do veio coincide com uma frequência natural e produz uma ressonância. Isto aparece como um pico de amplitude e mudança de fase no gráfico do Bodé.
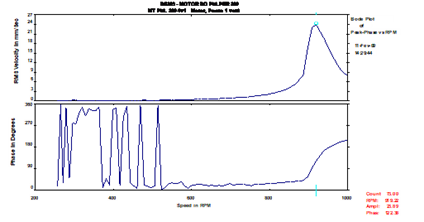
A identificação de frequências naturais é especialmente crítica nas turbomáquinas porque, ao contrário da maioria dos equipamentos de uso geral, funcionam acima ou perto de uma, se não mais, frequências naturais ou modos. O gráfico de Bodé é mais poderoso na identificação de vibrações síncronas. Enquanto a vibração global pode ser traçada também em relação à velocidade do veio, o gráfico Bodé não é realmente uma ferramenta para identificar vibrações não-síncronas.
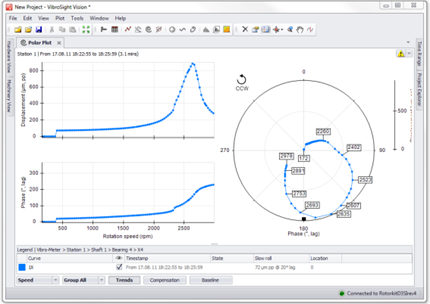
Processamento de dados de vibrações – O diagrama Polar (Nyquist)
O gráfico Polar apresenta exatamente os mesmos dados que o gráfico Bodé, apenas num formato de visualização diferente. Na parcela polar, a magnitude do vetor de deslocamento é medida radialmente, a partir do centro do gráfico e a fase é traçada circunferencialmente. Uma ressonância é indicada num gráfico pela velocidade a que a amplitude é a máxima de um circulo (ou seja, aproximadamente 180 graus de mudança de fase).
Processamento de dados de vibrações – A medição da Função de Resposta em Frequência
Esta função é usada para determinar as frequências naturais de uma estrutura a partir de um ensaio de impacto.
Este ensaio tem como base o princípio de que qualquer estrutura quando está livre, vibra as suas frequências naturais. Portanto, para observar as suas frequências naturais basta, por exemplo, efetuar um impacto na estrutura e observar a resposta vibratória.
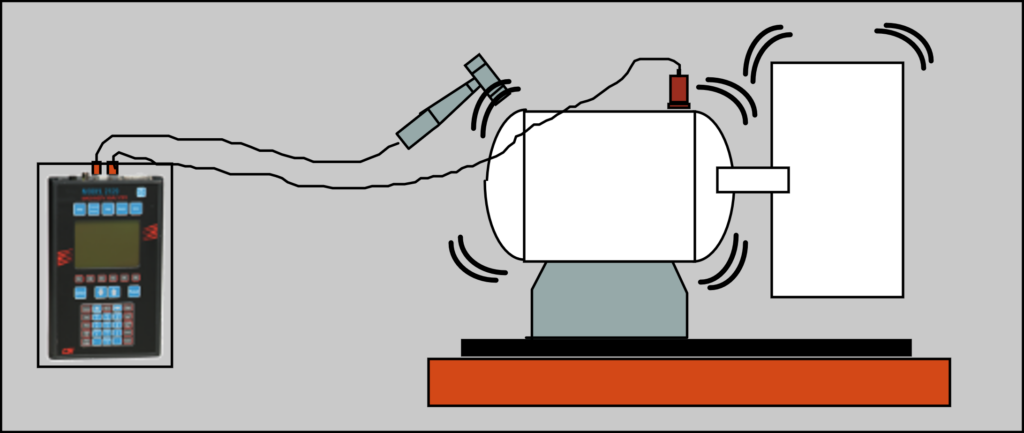
Existem duas formas de observar o impacto.
- A forma mais simples consiste em medir só a resposta; o designado ensaio de impacto.
- A forma mais elaborada consiste em medir a Função de Resposta em Frequência (FRF). Esta é obtida utilizando um martelo instrumentado com um transdutor de força de forma a se conhecer a energia que está a ser introduzida na estrutura. Esta forma de medir as frequências naturais é mais precisa e permite a comparação dos resultados medidos com os modelos de elementos finitos e a analise modal.
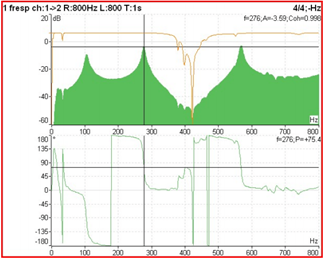
A medição da resposta em frequência (FRF) para alem de uma das funções atrás descritas proporciona informação sobre a fase das vibrações e a função coerência.
Numa medição da Função de Resposta de Frequência pode ser observado o seguinte:
- Ressonâncias – Os picos indicam a presença das frequências naturais da estrutura em teste;
- Amortecimento – O amortecimento é proporcional à largura dos picos. Quanto mais largo o pico, maior é o amortecimento;
- Modo de vibração – A amplitude e fase de múltiplas FRFs adquiridas relativamente a uma referência comum numa estrutura são utilizados para determinar a forma do modo.
A Coerência é função versus frequência, que indica quanto da saída é devido à entrada na FRF. Pode ser um indicador da qualidade da FRF. Avalia a consistência do FRF desde a medição até à repetição da mesma medição. O valor de uma função de coerência varia entre 0 e 1.
A medição de fase, define inequivocamente que estamos na presença de uma frequência natural pois, na ressonância a fase varia 180º. Caso esta variação seja inferior a 180º quer dizer que, ou a estrutura está fortemente amortecida ou então, que o movimento da estrutura na ressonância não ocorre na direção do acelerómetro e/ou do martelo.
Processamento de dados de vibrações, configuração do Analisador FFT e Coletor de Dados
O objetivo da configuração do analisador FFT é produzir dados sobre os quais possam ser tomadas decisões relativas a avarias e condição de funcionamento. O conhecimento da máquina é essencial; isto é, frequências de avarias, frequências naturais, e amplitudes de falhas críticas. É bem conhecido que todos estes dados não estarão disponíveis quando uma máquina é monitorizada ou analisada pela primeira vez. Contudo, à medida que o tempo passa e o analista trabalha com uma máquina, a experiência adquirida fornecerá informação acerca dos níveis de vibração nos quais aparecem defeitos que conduzem a avaria. A informação de frequências relativas a falhas como a velocidade do veio, frequências de rolamentos, frequências de passagem de lâminas ou pás, e frequências de engrenamento deveriam estar disponíveis no início da monitorização ou da análise. É, portanto, possível fazer uma razoável configuração a partir apenas dos dados do projeto. As duas principais questões que devem ser consideradas são resolução (frequências) e gama dinâmica (amplitudes).
Processamento de dados de vibrações e resolução do espetro
A resolução do espectro está dependente do número de linhas usado no cálculo FF (o qual está relacionado com o número de amostras da forma de onda no buffer de entrada, o intervalo de frequência, e a janela escolhida. A frequência resolúvel mínima é o inverso do tempo de aquisição de dados. Por outras palavras, deve estar presente no bloco de dados, um bloco completo (um período) de dados à frequência em questão, antes de essa frequência ser observada no espectro.
Por exemplo, pretende-se analisar dados a uma frequência de uma velocidade de funcionamento de 1800 RPM (30 Hz), então [1/30 = 0.033 s/ciclo]. Um mínimo de 33 ms de dados, deve ser recolhido. Caso contrário, a vibração a 30 Hz não fez um ciclo durante o processo de aquisição de dados.
Entre linhas não se podem separar frequências. Este facto é importante no relacionamento do intervalo de frequência e número de linhas para a frequência resolúvel mais baixa. Se forem escolhidas 400 linhas, o espectro será dividido em 400 pontos discretos, com todas as frequências a ficarem entre as linhas carregadas na sua linha adjacente. O analisador mostra a frequência no centro do bin. Por exemplo, se um intervalo de frequência de 1000 HZ tivesse sido escolhido no exemplo, a frequência resolúvel mais baixa seria 1000Hz/400 linhas, ou 2,5 Hz. Portanto deveria ter sido recolhido, 400 ms (1/2,5 = 0,40 segundo) de dados, e 30 Hz podia ser determinado.
Processamento de dados de vibrações – Erros e ruído devidos às janelas
São introduzidos erros e ruído quando são utilizadas janelas em processamento FFT. Por esta razão um fator de janela (fator de ruído) é usado para calcular a resolução garantida. A resolução teórica do intervalo de frequência dividido pelo número de linhas deve assim ser diminuída multiplicando por duas vezes o fator de janela.
Quando um coletor de dados é usado para conduzir diagnóstico de avarias ou avaliação da condição, deve ser guardada uma forma de onda com cada espectro. Se os dados estiverem a ser gravados, os dados guardados devem ser suficientes de modo que a análise FFT possa ser conduzida para os intervalos de frequência e resolução desejados.