Analizador de vibraciones 5 – ventanas
Analizador de vibraciones 5 – ventanas
Seguidamente, en analizador de vibraciones 5, presentamos el tema de las ventanas en la forma de onda (“Ventanas”), cuando tienen lugar Para la implementación de esta técnica se requiere la existencia de un sensor taquimétrico que informe permanentemente al equipo de medición sobre la velocidad de rotación del eje donde se están realizando las mediciones. fácilmente los diferentes niveles de vibración en el zapato y el taco.. tan, este artículo es parte de una serie de artículos que explican cómo funciona un analizador de vibraciones.
Cuando lo hacemos Análisis de vibraciones, necesitamos entender cómo funciona un analizador. Por eso, aquí presentamos los conceptos de análisis de señales digitales, implementado en un analizador FFT. Para que sea fácil de entender, los presentamos siempre desde el punto de vista del usuario, a través de la observación de los resultados de mantenimiento predictivo.
Seguidamente, No hay enlace, podemos ver a gama de analizadores de vibración proporcionado por D4VIB.
En seguida, en Analizador de vibraciones 5, presentamos el contenido de esta serie de artículos.
-
- ¿Cuál es la relación entre tiempo y frecuencia?
- Cómo funciona el muestreo y el escaneo
- Qué es el aliasing y qué efectos tiene
- Cómo se usa y en qué consiste el zoom
- Cómo se utilizan las ventanas de forma de onda
- ¿Cuáles son los promedios para
- ¿Qué es el ancho de banda en tiempo real?
- Para que sirve el procesamiento de superposición ("superposición")
- Que es el seguimiento de pedidos
- Que es el análisis de envolvente
- Las funciones de dos canales en el dominio de la frecuencia
- Para que sirve Orbit
- ¿Cuáles son las funciones de un canal en el dominio del tiempo?
- En qué consiste el Cepstro
- ¿Cuáles son las unidades y escalas del espectro?
5 Analizador de vibraciones 5 – La implementación de las ventanas de la forma de onda (ventanas)
5.1 La necesidad de ventanas
Paralelamente, lo que se dijo anteriormente sobre aliasing, hay otra propiedad FFT, que afecta su uso en el análisis de dominio de frecuencia. Recordemos, que la FFT calcula el espectro de frecuencias, de un conjunto de muestras de la entrada, designado un bloque de tiempo.
5.1.1 ¿Qué sucede cuando la forma de onda es periódica en el bloque de tiempo?
Para empezar, vale la pena mencionar, que la FFT se basa en el supuesto de que el bloque de tiempo, se repite en el tiempo.
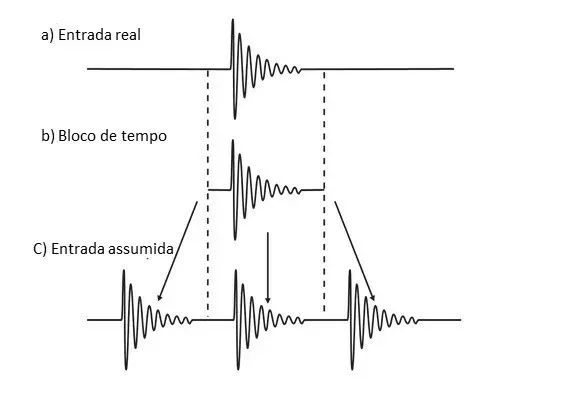
Figura 5.1. O FFT, parte del principio, que el bloque de tiempo / forma de onda, se repite en el tiempo.
De facto, con la vibración transitoria, de la figura anterior, esto no causa ningún problema.
Por otro lado, ¿qué sucede si está midiendo una señal continua??
Tomemos, por ejemplo, el caso de que estamos midiendo una onda de un seno.
Veamos la situación en la que el bloque de tiempo contiene un número entero de ciclos de ondas sinusoidales. Entonces en este caso el bloque de tiempo se repite indefinidamente, y es de facto, a onda real.
tan, en este caso, la forma de onda de entrada es periódica en el bloque de tiempo.
Figura 5.2. En esta situación la señal de entrada es periódica en el bloque de tiempo..
5.1.2 ¿Qué sucede cuando la forma de onda no periódica en el bloque de tiempo
Por lo contrario, cuando la entrada no es periódica en el bloque de tiempo, la figura de abajo, muestra la dificultad con esta suposición.
En esta situación, la FFT se calcula basándose en la forma de onda altamente distorsionada que vemos en c).
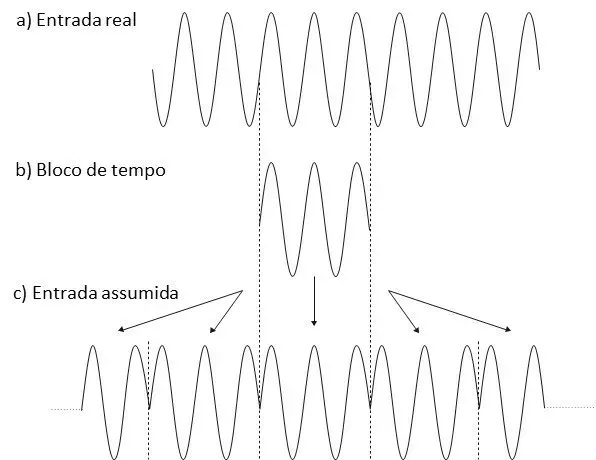
Figura 5.3. En esta figura vemos la forma de onda no periódica en el bloque de tiempo..
5.1.3 Que son las fugas
Sabemos que cuando la forma de onda es un seno, el espectro de frecuencia tiene una sola línea. Por lo contrario, sabemos que los fenómenos abruptos en un dominio, se extienden por el otro dominio.
Seguidamente, en la figura, vemos que estas consideraciones son correctas en una medida real. En las figuras un) & segundo), ves una forma de onda que es periódica en el bloque de tiempo. tan, su espectro de frecuencia es una sola línea cuyo ancho está determinado solo por la resolución de nuestro analizador. Por otro lado, nas figuras c) yd) vemos una forma de onda sinusoidal que no es periódica en el bloque de tiempo. Como se predijo, su energía se extendió por todo el espectro, .
una) e b) – Onda sinusoidal periódica en el bloque de tiempo
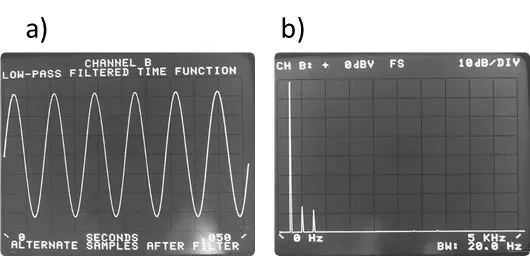
do) yd) – Onda sinusoidal no periódica en el bloque de tiempo
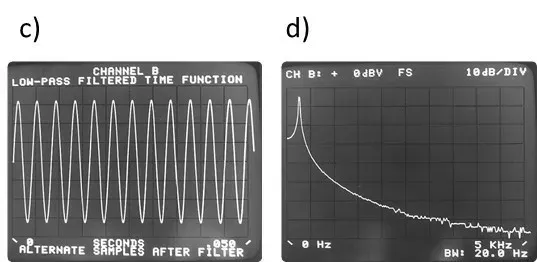
Figura 5.4 Resultados reales de la transformación FFT.
tan, esta dispersión de energía, en todos los dominios de frecuencia, Es conocido como escapar (fuga). en realidad, como su nombre indica, vemos fugas de energía, de una línea de espectro, para todas las demás líneas.
5.1.4 Resultado de fugas?
Hay que ver que, las fugas de energía se deben al hecho de tener un bloque de tiempo finito. De facto, para que una onda sinusoidal tenga un espectro de una sola línea, debe existir para siempre, de menos infinito a más infinito. Si tuvieras un bloque infinito de tiempo, la FFT calcularía el espectro correcto, con una sola línea. Sin embargo, un registro de tiempo finito de la onda sinusoidal solo se observa porque no estamos dispuestos a esperar para siempre, para medir un espectro. tan, esto puede causar fugas si la entrada continua no es periódica, en el bloque de tiempo.
Es obvio, de la observación de la figura 5.4, que el problema de las fugas es lo suficientemente grave como para enmascarar completamente los pequeños signos, cerca de las ondas sinusoidales más grandes. En estas circunstancias, el algoritmo de cálculo del espectro de frecuencia FFT no proporciona un analizador de vibraciones útil.
5.2 UNAanalizador de vibraciones 5 – ¿Qué son las "ventanas"??
Para solucionar este problema, a seguir, en Analizador de vibraciones 5, veamos cómo se implementa una solución conocida como "windows"( “Ventanas” en ingles).
en la figura 5.5 ( a e b) reproducimos la forma de onda de entrada de un seno que no es periódico en el bloque de tiempo.
En este caso, notamos que la mayor parte del problema parece estar en ambos lados del bloque de tiempo. De facto, en la situación actual, el centro es una onda sinusoidal, bien representado.
tan, si la FFT pudiera ignorar los extremos y enfocarse en el medio del bloque de tiempo, uno esperaría estar mucho más cerca del espectro de una sola línea, cual es correcta.
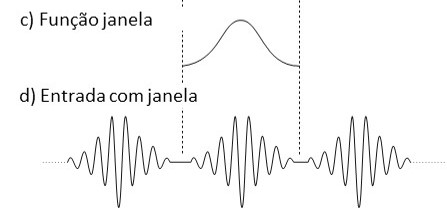
Por ejemplo, si multiplicamos el bloque de tiempo por una función, que es cero en los extremos del bloque y grande en el medio, el resultado del cálculo de FFT sería principalmente de la mitad del bloque de tiempo.
en la figura 5.5 do) vemos una de estas funciones.
El nombre de estas funciones es "funciones de ventana". Efectivamente, estas funciones te obligan a mirar los datos, a través de una ventana estrecha.
Figura 5.5. – tu c) yd), vemos un “función de ventana” y su efecto en la forma de onda que se utilizará para calcular la FFT.
5.3 El efecto de la función de ventana.
Efectivamente la figura 5.6, muestra la gran mejora que se ha obtenido aplicando ventanas a datos que no son periódicos en el bloque de tiempo.
Sin embargo, Es importante darse cuenta de que los datos de entrada han sido alterados y no podemos esperar resultados perfectos.. Siguiente en Analizador de vibraciones 5, veamos esta pregunta.
La FFT asume que la forma de onda se parece a la Figura 5.5 re). En otras palabras, la FFT asume la forma de onda como un seno de amplitud modulada. Esto genera un espectro de frecuencias, que está más cerca de la línea correcta de la onda de entrada sinusoidal que la Figura 5.5 segundo), pero aun no es correcto.
De facto, a Figura 5.6 do) muestra que los datos con Windows no tienen un espectro con una línea tan estrecha, cuanto una función, sin ventana, que es periódico en el bloque de tiempo.
una) Onda sinusoidal no periódica dentro del bloque de muestra de tiempo
segundo) FFT resultante sin función de ventana
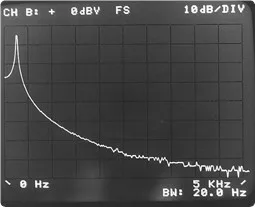
do) Resultados de FFT con una función de ventana de figura 5.6. Reducción de fugas mediante ventanas en el bloque de tiempo
Figura 5.6 Reducción de fugas mediante ventanas en el bloque de tiempo
5.4 Una janela Hanning
Hay muchas funciones que se pueden utilizar para implementar ventanas en muestras en la forma de onda.. Siguiente en Analizador de vibraciones 5, veamos esto los tipos de ventanas.
De facto, el más común se llama Hanning.
La ventana de Hanning se utilizó en la Figura 5.7, como ejemplo de reducción de fugas con ventanas.
La ventana de Hanning también se usa comúnmente para medir vibraciones con ruido aleatorio.. Por ejemplo, este es el caso de las vibraciones estacionarias que medimos en las máquinas.
una) Medición sin fugas – entrada periódica en el bloque de tiempo
segundo) Medida con ventana – entrada no periódica en el bloque de tiempo
Figura 5.7. La función de ventana reduce las fugas, pero no los elimina
5.5 La ventana del uniforme (también llamado rectangular)
5.5.1 Una limitación de la ventana de Hanning
Se vio que la ventana de Hanning hace un trabajo aceptable en los ejemplos de onda sinusoidal., tanto periódicas como no periódicas en el registro de tiempo. Si esto es cierto, por qué usar otras ventanas?
Suponer que, en lugar de querer el espectro de frecuencia de una señal continua, si desea obtener un espectro para un evento transitorio.
Para este fin, en la figura 5.8 una) mostramos una vibración transitoria típica. Si se multiplica por la función de la ventana en la figura 5.8 segundo), obtendría la señal altamente distorsionada que se muestra en la figura 5.8 do).
una) Espectro de vibraciones transitorias sin ventana
segundo) Espectro de vibraciones transitorias con ventana de Hanning
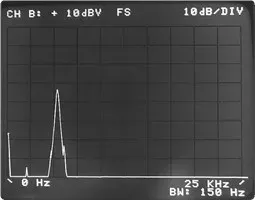Figura 5.8 Como se mencionó aquí, vemos que la función de la ventana de Hanning, pierde información sobre eventos transitorios.La ventana de Hanning transformó lo transitorio. Es, que tiene energía distribuida ampliamente en el dominio de la frecuencia, se parecía más a una onda sinusoidal.
por lo tanto, podemos ver que para los fenómenos transitorios no queremos usar la ventana de Hanning.
5.5.2 La ventana Uniforme
Nos gustaría utilizar todos los datos en el bloque de tiempo por igual o uniformemente.
Por lo tanto, si usa la ventana uniforme que pesa todo el bloque de tiempo por igual.
Observa la figura 5.8, que el transitorio tiene la propiedad de tener un valor de cero al principio y al final del bloque de tiempo. Recuerde que las ventanas se introdujeron para forzar la entrada a cero. en los extremos de la bloque de hora. En este caso, no es necesario usar la ventana en la entrada.
5.6 Señales de ventana automática
Cualquier letrero como este, se llama "ventana automática", porque no requiere ventana. Esto es efectivamente tan, porque ocurre completamente dentro de un bloque de tiempo. Estas señales no generan fugas en la FFT y por tanto no necesitan ventana.
Hay muchos ejemplos de señales de "ventana automática", algunos de los cuales mostramos en la Figura 5.10.
El análisis de frecuencia de las siguientes señales se puede realizar sin ventana, debido al hecho de que son señales de ventana automática:
- Impactos,
- Impulsos,
- Respuestas al choque,
- Ráfagas de seno, ruido o impulsos
- Ruido pseudoaleatorio
Figura 5.10. En esta figura vemos ejemplos de señales de ventana automática.
5.7 La ventana superior plana "Flat Top"
Anteriormente vimos que necesita una ventana uniforme, para analizar funciones de ventana automática, como el ejemplo de las vibraciones transitorias.
Además, necesitamos una ventana de Hanning para medir el ruido y las señales periódicas, como ondas sinusoidales.
Ahora es necesario introducir una tercera función de ventana.. Así que ahora te presentamos, una ventana superior plana, para evitar un efecto de ventana de Hanning.
5.7.1 Limitaciones de la ventana Hanning
Para entender este efecto, necesitas mirar la ventana de Hanning en el dominio de frecuencia.
Recuerde que la FFT actúa como un conjunto de filtros paralelos. A figura 5.11 muestra la forma de esos filtros, al usar la ventana de Hanning. Podemos ver que la función Hanning le da al filtro, una parte superior muy redondeada. En esta situación, si un componente de frecuencia de la señal analizada, caer en el centro en el filtro, su nivel se medirá con precisión. Caso contrário, la forma del filtro atenuará el componente hasta que 1,5 dB (16%), cuando cae en el medio del espacio entre los filtros.
Figura 5.11. – En esta figura vemos como la ventana de Hanning atenúa la amplitud del componente de frecuencia.
De facto, al intentar medir la amplitud de una señal, exactamente, este error es muy grande.
5.7.2 La precisión de medición de la ventana superior plana.
Entonces tenemos que la solución a este problema, es elegir una función de ventana que le dé al filtro una parte superior más plana.
Figura 5.12 Se muestra esta forma con una parte superior más plana..
en realidad, el error de amplitud de esta ventana no excede 0,1 dB (1%). De este modo, precisión de la medición, obtuvimos una mejora de 1,4 dB.
5.7.3 La reducción de resolución de la ventana superior plana
Cabe señalar que mejorar la precisión en la medición del nivel, no viene sin precio.
A figura 5.15 muestra que la parte superior de la ventana se ha aplanado, a expensas de ensanchar los faldones del filtro. Por eso, Perdimos algo de capacidad de resolución y la habilidad de observar un pequeño componente., cerca de un gran.
Algunos analizadores de vibraciones ofrecen comandos y funciones desde la ventana "plana". De esta forma podemos elegir entre una mayor precisión para equilibrar el trabajo, por ejemplo, o resolución de frecuencia, mejorado, desde la ventana "Hanning".
Figura 5.13. En esta figura vemos la resolución reducida de la ventana plana.
5.8 Analizador de vibraciones 5 – Otras funciones de ventana
Hay muchas otras funciones de ventana., pero los tres enumerados anteriormente son los más comunes para las medidas generales. Sin embargo, para situaciones especiales de la medida, otros grupos de funciones de ventana pueden ser útiles.
Las siguientes son dos ventanas que son particularmente útiles, al medir la respuesta de frecuencia de estructuras mecánicas, mediante pruebas de impacto.
5.8.1 Prueba de impacto – las ventanas de fuerza y respuesta
A menudo se usa un martillo instrumentado, impactar una estructura y hacerla vibrar a su frecuencia natural.
Para medir la fuerza del impacto, en la parte superior del cabezal de impacto del martillo, se coloca un transductor de fuerza. Por lo tanto, los martillos instrumentados se utilizan para determinar las frecuencias naturales y medir la respuesta de frecuencia..
ordinariamente, la entrada de energía está conectada a un canal del analizador y la respuesta de la estructura, medido con un acelerómetro, está conectado a otro canal.
Este impacto de la fuerza es obviamente una función de ventana automática. La respuesta de la estructura también es ventana automática.. De hecho, esto es así si la señal desaparece dentro del bloque de tiempo del analizador.
5.8.2 La ventana de respuesta
Para garantizar que la respuesta llegue a cero al final del bloque de tiempo, a veces se agrega una ventana exponencial. tan, esta ventana se llama ventana de respuesta.
A Figura 5.14 muestra una ventana de respuesta, actuando sobre la respuesta de una estructura débilmente amortiguada.
Debido a que la estructura está mal amortiguada, la vibración no disminuyó por completo hasta el final del bloque de tiempo.
Observe-se que, a diferencia de la ventana de Hanning, el valor de la ventana de respuesta no es cero, en ambos extremos del bloque de tiempo.
Se sabe que la respuesta de la estructura será cero al comienzo del bloque de tiempo. (antes de que golpeara el martillo). Visto esto, no es necesario que la función de ventana sea cero.
Además, sabemos que la mayor parte de la información sobre la respuesta estructural, está contenido al principio del bloque de tiempo. Por esto, es necesario asegurarse de que esta área, ser más tenido en cuenta, por la función de ventana de respuesta.
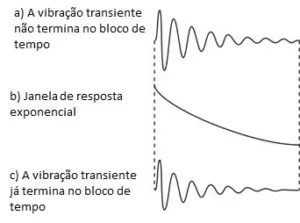
Figura 5.14. En esta figura vemos cómo se utiliza la ventana exponencial..
5.8.3 La ventana de fuerza
El bloque de tiempo de la fuerza excitante, solo debe ser la señal de impacto con la estructura. Sin embargo, el movimiento del martillo antes y después de golpear la estructura, puede causar ruido en el bloque de tiempo.
Para evitar esto usamos una ventana eléctrica. tan, podemos ver esto en la figura 5.15.
La ventana de fuerza tiene un valor igual a la unidad, donde los datos de impacto son válidos y cero en cualquier otro lugar. Esto es efectivamente tan, para que el analizador no mida ningún ruido, que puede estar presente.
Figura 5.15. -Aquí vemos cómo se utiliza la ventana de fuerza..
5.9 – Formas de filtro de paso de banda o funciones de ventana?
Como se mencionó anteriormente, a veces se hace referencia a funciones de ventana en el dominio del tiempo. En otras ocasiones, Se hizo referencia al tema utilizando la referencia a la forma de filtros de paso de banda en el dominio de la frecuencia., causado por estas ventanas. En ambas situaciones, la perspectiva se cambió libremente al dominio que produce la explicación más simple..
De la misma forma, algunos analizadores de vibraciones llaman uniforme a las ventanas, hanning e flat-top “ventanas” y otros analizadores llaman a estas funciones "formas de paso de banda”.
De hecho, usamos la terminología que es más fácil para el problema en cuestión.. Esto se debe a que son completamente intercambiables.. Del mismo modo, los dominios de tiempo y frecuencia son completamente equivalentes.
Por ejemplo, en la especificación del analizador de vibraciones. ADASH 4500VA se refiere a tener las siguientes ventanas: Rectangular, Hanning, Exponencial, Transitorio.
